Lógica Multidimensional:
Un modelo de lógica paraconsistente
Carlos Gershenson
E-mail: cgg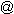
unam.mx
http://turing.iimas.unam.mx/%7Ecgg/jlagunez/aniei98/lmd.html
Fundación Arturo Rosenblueth
"Sobre un hecho hay tantas verdades
como conjuntos hay en el universo...
y mentiras, muchas más"
Resumen
La lógica multidimensional es un nuevo sistema de lógica propuesto para modelar lógica paraconsistente. Una breve definición de lógica paraconsistente y ejemplos de cuando es usada son dados. Se definen los principios y propiedades de la lógica multidimensional, tales como las variables lógicas multidimensionales. Los operadores lógicos Y, O, NO, SI... ENTONCES y SÍ Y SÓLO SI son definidos y explicados para la lógica multidimensional. Además, se definen equivalencia, grado de contradicción, y la proyección de la lógica multidimensional en la difusa. Esto incluye un pequeño programa que usa lógica multidimensional.
Introducción
Hasta hace unos años, la gente trataba de restringir las reglas que provocaban paradojas y antinomias [7]. Entonces la lógica paraconsistente fue desarrollada para comprender mejor las contradicciones en vez de tratar de excluirlas. Una lógica se dice que es paraconsistente si admite que una conclusión sea obtenida de premisas contradictorias [6]. Por ejemplo:
Si A y ~A entonces B
Otro ejemplo sería la llamada paradoja del mentiroso:
Esta frase es falsa.
Si la frase es verdadera, entonces dice que es falsa. Pero si es falsa, nos dice que es falsa su falsedad, y por lo tanto, verdadera. Lógicas paraconsistentes admiten esta y otros tipos de contradicciones.
Un tercer ejemplo está basado en una versión del primer teorema de la incompletitud de Kurt Gödel:
Esta frase no es probable.
Esta es similar a la paradoja del mentiroso. Si la frase es probable, entonces es verdadera, y por lo tanto, no probable. Y si no es probable, entonces la frase sería probada.
Finalmente, veamos la llamada paradoja o antinomia de Russell:
Un conjunto que no se tiene a sí mismo como uno de sus elementos se dice que es respetable.
Sea R el conjunto que contiene a todos los conjuntos respetables.
Es R respetable?
Si R es respetable, contiene a todos los conjuntos respetables, y por lo tanto, se contiene a sí mismo, y no es respetable. Si R no es respetable, dado que R contiene a todos los conjuntos respetables, R no se contiene a sí mismo, y es respetable.
Hay libros enteros acerca de paradojas, pero con estos ejemplos hemos visto, que hay muchos casos donde un sistema lógico consistente fallaría en llegar a una conclusión.
Las lógicas clásica, intuicionista, booleana y difusa, sólo encuentran es estos ejemplos una contradicción o paradoja. La lógica multidimensional es desarrollada para comprender contradicciones, tal como lo hace la lógica paraconsistente, y para hacer operaciones con ellas, como en las lógicas booleana y difusa.
¿Por qué multidimensional?
La lógica multidimensional le asigna un vector de verdad a un hecho, en vez de sólo un valor. Este nombre fue propuesto porque existe la idea de extender el modelo de más de un valor de verdad no sólo para dos (como actualmente está), sino para n. La idea no está lo suficientemente madura para ser expuesta aquí, pero existe la intención de generalizar el modelo actual.
Lógica multidimensional
A continuación definiremos variables lógicas multidimensionales (vlmd):
X es una vlmd sí y sólo si X M={(x,y) | x,y [0,1]}
Este es un vector bidimensional, del que cada elemente se encuentra en el intervalo [0,1]. Podemos representar una vlmd en el siguiente plano (similar al de los números complejos):
Al contrario que en la lógica lineal (booleana y difusa, no la lógica lineal de Girard), la lógica multidimensional acepta más de un valor de vardad. Puede manejar contradicciones e incertidumbres. La línea azul que va de (0,1) a (1,0) representa a la lógica difusa. La llamaremos "línea difusa", ya que la mencionaremos más adelante. Esta línea es el conjunto de los puntos cuyas coordenadas se complementan (su suma es 1), y por lo tanto, no hay contradicción. Cada eje representa una condición. Por ejemplo, verdadero y falso. Entonces, cuando el valor de verdad complemente el de falsedad, no habrá contradicción, y la lógica difusa se podrá encargar de estos casos. Por ejemplo, la paradoja del mentiroso:
Esta frase es falsa.
No puede ser manejada con lógica difusa. Decimos, como en la lógica multi-valuada de Asenjo [1], que es verdadera Y falsa. Le podemos asignar el vector de verdad (1,1).
Operadores Lógicos Multidimensionales
Ahora podemos definir los operadores lógicos multidimensionales Y (&), O (|), y NO (~). Nos basamos en los operadores lógicos difusos propuestos inicialmente por Lotfi Zadeh [8]. (El O es inclusivo).
Al aplicar los operadores lógicos difusos elemento a elemento de un vector de verdad, obtendremos los operadores lógicos multidimensionales. Esto es:
(x1,y1) & (x2,y2) = (x1 & x2, y1 & y2) = (min(x1,x2), min(y1,y2))
(x1,y1) | (x2,y2) = (x1 | x2, y1 | y2) = (max(x1,x2), max(y1,y2))
~(x1,y1) = (~(x1), ~(y1)) = (1-x1, 1-y1)
Ahora veamos unos ejemplos con las siguientes proposiciones:
(verdadera) Esta frase es falsa (1,1)
(verdadera) Esta frase es verdadera (1,0)
Podemos concluir que:
Esta frase es verdadera y falsa (1,0)
Nótese que el vector de verdad (1,0), es concluido al razonar las proposiciones, no la conclusión.
Además, podemos concluir que:
Esta frase es verdadera o falsa (1,1)
Esta conclusión, como en el ejemplo pasado (y cualquier razonamiento lógico), es obtenida al razonar sólo las proposiciones.
Para la negación, podemos observar que para cualquier vlmd (x,y), su negación está en la recta que pasa por (x,y) y (0.5, 0.5) y está a la misma distancia de la que está (x,y) de (0.5, 0.5), pero en sentido opuesto.
Para el SI...ENTONCES (->), y SÍ Y SÓLO SI (<->), usamos las proposiciones equivalentes:
A -> B = ~A | B
A <-> B = (A->B) & (B->A))
Y en base a esto definimos:
(x1,y1) -> (x2,y2) = (max ((1-x1),x2),max ((1-y1),y2))
(x1,y1) <-> (x2,y2) = (min(max((1-x1) ,x2), max((1-x2), x1),max((1-y1), y2),max((1-y2), y1)))
Como estos dos últimos operadores, podemos definir otros en términos de &, | y ~. Por ejemplo, un O exclusivo (XOR), puede verse como:
A XOR B = ~(A <->B)
Equivalencia
Si se "doblara" el plano en la línea difusa, los puntos que estarían uno junto al otro, serían equivalentes. Para mostrar un ejemplo, podemos fijar las vlmd como (verdadero, falso). (0,0) y (1,1) son equivalentes. Esto es porque si el grado de falsedad es 0, significa lo mismo que el de verdad sea 1; y si el de verdad es 0, que el de falsedad sea 1. Lo mismo pasa con (0.25,1) y (0, 0.75). Podemos definir la equivalencia como:
E(x,y)=(1-y,1-x)
También podemos ver que:
E(x,y)=(~y,~x)
Nótese que los vectores sin contradicción (de la línea difusa), son sus propios equivalentes. También nótese que para todos los puntos en la recta x=y, su negación es la misma que su equivalente. Y como (0.5, 0.5) es su propio equivalente, también es su propia negación. Además, nótese que
A & B = E(A | B)
A | B = E(A & B)
Grado de Contradicción
Sea (x, y) una vlmd. Podemos definir el grado de contradicción C como:
C(x,y)=|(x+y)-1|
C puede verse como "qué tan lejos se va de la lógica difusa". Si C es 0 (no hay contradicción), entonces el punto pertenece a la línea difusa, y es contenido por la lógica difusa. Al incrementar C, uno se aleja de la línea difusa, hasta llegar a una contradicción total (C=1). Con C, podemos ver "qué tan contradictoria es una proposición.
Nótese que C es una función que va de ([0,1],[0,1]) a [0,1].
Dunn propuso una lógica multi-valuada con 4 valores de verdad [2]: verdadero, falso, verdadero y falso, y ni verdadero ni falso. Podemos asignarles los vectores (1,0), (0,1), (1,1), y (0,0). Y ya hemos visto que estos dos últimos son equivalentes.
Proyección en la Lógica Difusa
Podemos usar como ejemplo una gráfica de algo que es blanco Y negro al mismo tiempo, o ninguno de los dos.
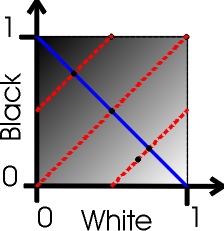
Si el valor de blanco es 0, entonces es considerado como negro. Si el valor de negro es 0, entonces es considerado como blanco. Aquí pudiese parecer que todos los puntos de las rectas paralelas a la recta x=y fuesen equivalentes. Esto es porque el blanco y negro son agregados, pero no se puede ver en la gráfica el total de contradicción. Por ejemplo, en (1,1), decimos que tenemos 100% blanco y 100% negro. Esto nos da gris. El mismo tono de gris que en (0.5, 0.5). Pero no es lo mismo 100% gris que 200% gris.
También podemos observar la proyección de lógica bidimensional en lógica difusa. Esto es, el "tono" de verdad que una contradicción tendría en lógica difusa. Pero, como dijimos, no es equivalente. La podemos encontrar al trazar una recta paralela a la recta x=y, o sea, de pendiente 1, que pase por el punto que se quiera proyectar. Entonces, la proyección sería su intersección con la línea difusa.
De esta forma, podemos encontrar la proyección de contradicciones en la lógica difusa. Por ejemplo, en la paradoja del mentiroso, la cual es verdadera y falsa, decimos que tiene un vector de verdad de (1,1). Su proyección seria (0.5, 0.5). Esto es, mitad cierto, mitad falso.
Podemos ver que la proyección P(x1, y1) es la solución al sistema
y-y1=x-x1
y=1-x
Estas ecuaciones son de las rectas que deben intersectarse en el punto de proyección. Al resolver el sistema, podemos ver que
P(x1,y1) = ((x1-y1+1)/2,(y1-x1+1)/2)
Precedencia de operadores
Los operadores monádicos (~, C, E, P) tienen prioridad sobre los diádicos (&, |, ->, <->). Para operadores del mismo nivel de precedencia, debe haber un paréntesis indicando qué operación va primero. Podemos ver que si A, B y C son vlmd,
(A & B) | C A & (B | C)
Propiedades del Y y del O multidimensionales
Sean A, B, C vlmd. Veremos a continuación las propiedades de los operadores multidimensionales & y |.
Cerradura:
A & B = (min(a1,b1), min(a2,b2)) = (a1 ó b1, a2 ó b2)
Dado que A y B son vlmd, a1, b1, a2, y b2 [0, 1], y por lo tanto,
(A & B) también es una vlmd. :. QED
A | B = (max(a1,b1), max(a2,b2)) = (a1 ó b1, a2 ó b2)
Dado que A y B son vlmd, a1, b1, a2, y b2 [0, 1], y por lo tanto,
(A | B) también es una vlmd. :. QED
Elemento identidad:
Para & es (1,1) y para | es (0,0)
A & (1,1) = A
(min(a1,1), min(a2,1)) = (a1,a2) = A :. QED
A | (0,0) = A
(max(a1,0), max(a2,0)) = (a1,a2) = A :. QED
Elemento nulo:
Para & es (0,0) y para | es (1,1)
A & (0,0) = (0,0)
(min(a1,0),min(a2,0) = (0,0) :. QED
A | (1,1) = (1,1)
(max(a1,1),max(a2,1) = (1,1) :. QED
Conmutatividad:
A & B = B & A
(min(a1,b1),min(a2,b2)) = (min(a1,b1),min(a2,b2)) :. QED
A | B = B | A
(max(a1,b1),max(a2,b2)) = (max(a1,b1),max(a2,b2)) :. QED
Asociatividad:
(A & B) & C = A & (B & C)
(min(a1,b1),min(a2,b2)) & C = A & (min(b1,c1),min(b2,c2))
(min(a1,b1,c2),min(a2,b2,c2)) = (min(a1,b1,c2),min(a2,b2,c2))
:. QED
Podemos ver que la misma propiedad se aplica a |, y que
A1 & A2 & ... & An=(min(a11,a21,...,an1), min(a12,a22,...,an2))
A1 | A2 | ... | An=(max(a11,a21,...,an1), max(a12,a22,...,an2))
Distributividad:
A & (B | C) = (A & B) | (A & C)
A & (max(b1,c1), max(b2,c2)) = (min(a1,b1), min(a2,b2)) | (min(a1,c1), min(a2,c2))
(min(a1,max(b1,c1)), min(a2,max(b2,c2))) = (max((min(a1,b1),(min(a1,c1)), max((min(a2,b2),(min(a2,c2)))
Dado que min y max también sin distributivos,
(min(a1,max(b1,c1)), min(a2,max(b2,c2))) = (min(a1,max(b1,c1)), min(a2,max(b2,c2))) :. QED
Y de forma similar para A | (B & C) = (A | B) & (A | C).
Nótese que sólo hay un elemento inverso para &, su identidad (1,1)
(1,1) & (1,1) = (1,1)
y uno para |, también su identidad (0,0)
(0,0) | (0,0) = (0,0)
Leyes de De Morgan:
~(A&B) = ~A | ~B
~(min(a1,b1),min(a2,b2)) = (1-a1,1-a2) | (1-b1,1-b2)
Dado que las leyes de De Morgan también se aplican a min y max,
(max (1-a1,1-b1),max (1-a2,1-b2)) = (max (1-a1,1-b1),max (1-a2,1-b2))
:. QED
Y de manera similar para ~(A | B) = ~A & ~B.
Otras propiedades:
~(~A) = A
~(1-a1,1-a2) = A
(1-(1-a1),1-(1-a2)) = A
(a1,a2)= A :. QED
E(E(A)) = A
E(1-a2,1-a1) = A
(1-(1-a1),1-(1-a2)) = A
(a1,a2)= A :. QED
A | (A & B) = A
A | (min (a1,b1),min(a2,b2)) = A
(max(a1,min (a1,b1)),max(a2,min (a2,b2))) = A
(a1,a2)= A :. QED
Dualidad:
Podemos ver que si intercambiamos en una propiedad | por &, & por |, y una vlmd explícita (e.g. (1,1), no A), el resultado es otra propiedad, la dual de la primera. Por ejemplo, para esta última propiedad, podemos obtener su dual:
A | (A & B) = A
A & (A | B) = A
Otro ejemplo sería:
A & ~A = ~(A | ~A)
Podemos ver que esto se cumple para todas las propiedades recién mostradas. Un ejemplo rápido sería el elemento inverso:
(1,1) & (1,1) = (1,1)
~(1,1) | ~(1,1) = ~(1,1)
(0,0) | (0,0) = (0,0)
Ejemplos
En lógica difusa, al incrementar una medida, disminuimos su contraria en el mismo grado. Aquí, como podemos ver, el valor de juventud decrece, su opuesto, vejez, debe incrementarse al mismo ritmo. De otra manera, tendríamos una contradicción de cierto grado.
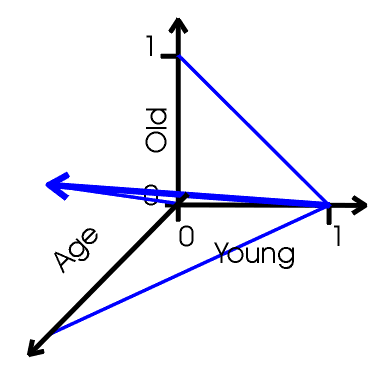
Pero en lógica multidimensional, una condición no necesariamente afecta su contraria. Así, podemos trazar distintos comportamientos para condiciones opuestas.
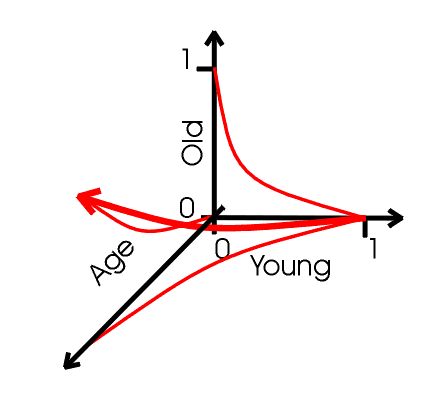
Basándonos en esta idea, un programa bastante sencillo fue hecho en C++ (mdlages.cpp). Pregunta acerca de ciertas gentes quién es mayor que quién, y quién es menor que quién. Usa lógica multidimensional para detectar contradicciones, y muestra los resultados que daría la lógica difusa, la multidimensional, y su proyección. El código y el ejecutable para DOS se pueden obtener en http://turing.iimas.unam.mx/%7Ecgg/jlagunez/mdl/mdlages.zip
Otro ejemplo pudiese ser una regla de alto-bajo con valores contradictorios. Podríamos decir que alguien es 0.7 alto y 0.5 bajo.
O cuando decimos: "me importa más la mujer que amo de lo que me importo yo mismo". Uno dice que le importa más su amada, pero eso es lo que le importa a uno.
Con esto, la lógica multidimensional puede ser bastante útil para muchos tipos de sistemas, los cuales necesitan cierta flexibilidad en sus procesos. Un ejemplo sería un sistema de soporte de toma de decisiones, con la capacidad de soportar contradicciones.
Conclusión
Como podemos ver, la lógica multidimensional es una herramienta valiosa para modelar lógica paraconsistente. Esto puede ser bastante útil en sistemas complejos los cuales pudiesen llegar a tener contradicciones, y ayudaría a encontrar la solución más adecuada al problema. Además, como fue mostrado en el programa mdlages.cpp, que se le puede asignar un significado "más lógico" a las contradicciones. La lógica multidimensional es útil hasta para detectarlas solamente.
Hay planes para definirla para más de dos dimensiones, y de definir los operadores aritméticos para la lógica multidimensional. ¿Quién sabe? Tal vez un día hasta podamos comprender a las mujeres.
Agradecimientos
Quisiera agradecer a Jaime Lagunez, Roberto Murcio, Jacobo Hernández, Raúl Rojas, y todos los que apoyaron, motivaron y criticaron este trabajo.
Bibliografía
