The Orthogonal Direction Change Chain Code
Chain-code techniques are widely used
because they preserve information and allow considerable data reduction, chain
codes are the standard input format for numerous shape analysis algorithms.
Using the orthogonal direction change chain code it is possible to represent
three-dimensional (3D) curves. Any 3D continuous curve can be digitalized and
represented as a 3D discrete curve. This 3D discrete curve is composed of
orthogonal constant straight-line segments. Thus, the chain elements represent
the orthogonal direction changes of the constant straight-line segments of the
discrete curve. The proposed chain code only considers relative direction
changes, which allows us to have a unique curve descriptor invariant under
translation and rotation. Also, this curve descriptor may be starting point
normalized for open and closed curves and invariant under mirroring
transformation.
Examples:

This curve was represented using the orthogonal direction change chain code.

A polygonal path of a Hilbert sequence represented by means of the orthogonal direction change chain code.
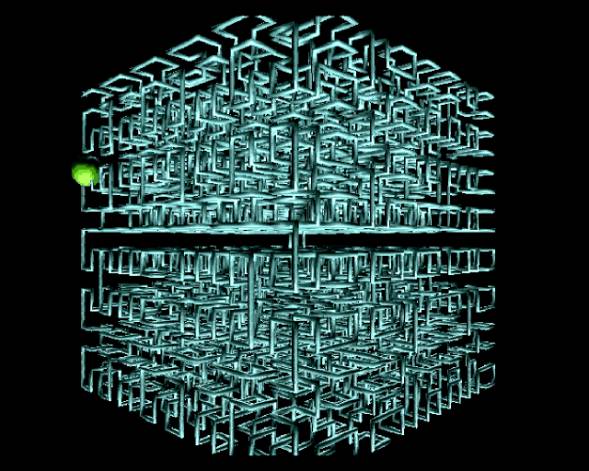
A polygonal path of a Hilbert sequence represented by means of the orthogonal direction change chain code.
References:
- Bribiesca E., A Chain Code for Representing
3D Curves, Pattern Recognition,
Vol. 33, No. 5, pp. 755-765 (2000).
- Bribiesca E. and Velarde C., A Formal
Language Approach for a 3D Curve Representation, Computers & Mathematics with Applications, Vol. 42, No.12,
pp. 1571-1584 (2001).
- Bribiesca E., Scanning-Curves Representation
for the Coverage of Surfaces Using Chain Coding, Computers &
Graphics, Vol. 27, pp. 123-132
(2003).
- Bribiesca E., 3D-Curve Representation by
Means of a Binary Chain Code, Mathematical and Computer Modelling,
Vol. 40 (3-4), pp. 285-295, (Aug 2004).