La máquina sin memoria
Memory can change the shape of a room; it can change the color of a car. And memories can be distorted. They're just an interpretation, they're not a record, and they're irrelevant if you have the facts. — Leonard Shelby, Memento
Hasta ahora
- Alfabetos, $\Sigma$
- Palabras, $w$
- Lenguajes, $L$
Para lenguajes
- Concatenación
- Unión
- Cerradura
esto es equivalente


$(\{b\}^*\{a\}\{b\}^*\{a\}\{b\}^*)^*$
Regresando al objetivo
Todas lás máquinas
Ya podemos hablar de todas las entradas: definimos un alfabeto, creamos cadenas, vemos las salidas...
El verdadero objetivo
Asociar lenguajes a un comportamiento de la máquina
Opciones
- Algunas cadenas de $L$ resultan en verdadero y otras falsos
- Todas las cadenas de $L$ resultan en verdadero
- Todas las cadenas de $L$ resultan en falso
Caso interesante
- Todas las cadenas resultan en verdadero
Si se dá, tendríamos una correspondencia entre máquina y lenguaje
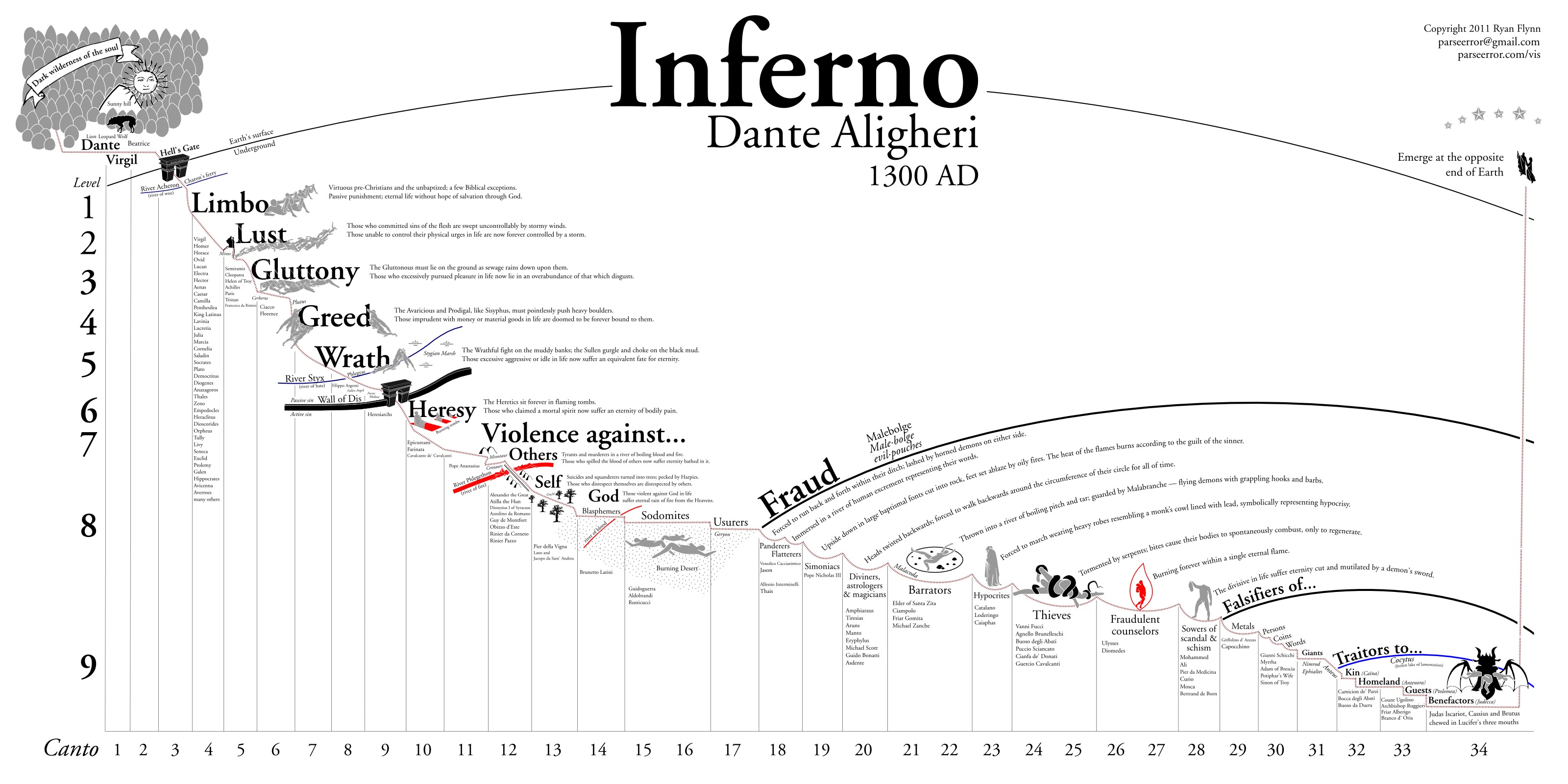
Los circulos de Dante
Jerarquía de Chomsky
Jerarquía de Chomsky
Lenguajes regulares
- Lenguages básicos
- Composición de lenguajes regulares
Lenguajes básicos regulares
- $\emptyset$, el lenguaje vacío, es regular
- $\{\epsilon\}$, el lenguaje de la cadéna vacía, es regular
- Si $a \in \Sigma$ entonces $\{a\}$, el lenguaje un símbolo del alfabeto, es regular
Composición de lenguajes regulares
- Si $L_1$ y $L_2$ son regulares, entonces $L_1 \cup L_2$ es regular
- Si $L_1$ y $L_2$ son regulares, entonces $L_1L_2$ es regular
- Si $L$ es regular, entonces $L^*$ es regular
- Si $L$ es regular, entonces $(L)$ es regular
Un lenguaje es regular si es un lenguaje básico regular o si se puede generar a través de una secuencia finita de operaciones de lenguajes regulares de lenguajess
El lenguaje regular de número de bes pares
Con $\Sigma=\{a,b\}$
Ejemplos:
- $bb$
- $bbabb$
- $aabbabb$
- $aabbabbaaaaaa$
- $aabaaababaabaaaaaa$
- $\{a\}$ y $\{b\}$
- $\{b\}\{a\}\{b\}$
- $\{b\}\{a\}^*\{b\}$
- $\{a\}\{b\}\{a\}^*\{b\}\{a\}$
- $\{a\}^*\{b\}\{a\}^*\{b\}\{a\}^*$
- $(\{a\}^*\{b\}\{a\}^*\{b\}\{a\}^*)^*$
Expresiones regulares
- Expresiones básicas
- Composición de expresiones regulares
Expresiones básicas regulares
- $\emptyset$ representa al lenguaje vacío
- $\epsilon$ representa al lenguaje de la cadéna vacía
- $a$ representa al lenguaje de un símbolo del alfabeto
Ésta es notación para representar lenguajes regulares básicos
Composición de lenguajes regulares
- $L_1+L_2$ representa a la unión de dos lenguajes
- $L_1L_2$ representa la concatenación
- $L^*$ representa a la cerradura sobre un lenguaje
- $(L)$ representa al lenguaje con prioridad
El lenguaje regular de número de bes pares
- $(\{a\}^*\{b\}\{a\}^*\{b\}\{a\}^*)^*$
Su expresión regular es:
- $(a^*ba^*ba^*)^*$
- $a^*(ba^*ba^*)^*$
El lenguaje regular cuyo penúltimo símbolo a
Un cambio de canal: ¡máquinas!


Autómata finito
Es una tupla $(Q,\Sigma,q_0,A,\delta)$
- $Q$ conjunto finito de estados
- $\Sigma$ un alfabeto
- $q_0$ estado inicial, $q_0 \in Q$
- $A$ conjunto de estados finales, $A \subseteq Q$
- $\delta$ función de transición $\delta:Q \times \Sigma \rightarrow Q$
Tambien conocida: Máquina de estados finitos
Estados, $Q=\{q_0,q_1\}$
Alfabeto, $\Sigma=\{a,b\}$
Estado inicial, $q_0$
Estados finales, $\{q_0\}$
Función de transición, $\delta$
En otras palabras
$\left(\{q_0,q_1\},\{a,b\},q_0,\{q_0\},\delta\right)$
donde $\delta=\begin{cases} (q_0,a) \rightarrow q_0 \\ (q_0,b) \rightarrow q_1 \\ (q_1,a) \rightarrow q_1 \\ (q_1,b) \rightarrow q_0 \\ \end{cases}$
Variaciones
En otras palabras
$\left(\{q_0,q_1\},\{a,b\},q_0,\{q_1\},\delta\right)$
donde $\delta=\begin{cases} (q_0,a) \rightarrow q_0 \\ (q_0,b) \rightarrow q_1 \\ (q_1,a) \rightarrow q_1 \\ (q_1,b) \rightarrow q_0 \\ \end{cases}$
En otras palabras
$\left(\{q_0,q_1\},\{a,b\},q_0,\{q_0,q_1\},\delta\right)$
donde $\delta=\begin{cases} (q_0,a) \rightarrow q_0 \\ (q_0,b) \rightarrow q_1 \\ (q_1,a) \rightarrow q_1 \\ (q_1,b) \rightarrow q_0 \\ \end{cases}$
Cadenas aceptadas por un AF
Definiendo función de transición extendida
$\delta^*=\begin{cases} \delta^*(q,\epsilon)=q & q \subseteq Q \\ \delta^*(q,wa)=\delta(\delta^*(q,w),a) &q \subseteq Q, w \subseteq \Sigma^*, a \subseteq \Sigma \\ \end{cases}$
Con la cadena: $abbaa$
- $\delta^*(q_0,abbaa) = \delta(\delta^*(q_0,abba),a)$
- $= \delta(\delta(\delta^*(q_0,abb),a),a)$
- $= \delta(\delta(\delta(\delta^*(q_0,ab)b),a),a)$
- $= \delta(\delta(\delta(\delta(\delta^*(q_0,a),b),b),a),a)$
- $= \delta(\delta(\delta(\delta(\delta(\delta^*(q_0,\epsilon),a),b),b),a),a)$
- $= \delta(\delta(\delta(\delta(\delta(q_0,a),b),b),a),a)$
- $= \delta(\delta(\delta(\delta(q_0,b),b),a),a)$
- $= \delta(\delta(\delta(q_1,b),a),a)$
- $= \delta(\delta(q_0,a),a)$
- $= \delta(q_0,a)$
- $= q_0$
Ya que $q_0$ pertence a $A$, la cadena es aceptada
Un automata $A$ acepta un lenguaje $L$
- Si $w\in L$ es aceptada por $A$
- Si $w\not\in L$ no es aceptada por $A$
Ejemplos
Concatenación
Cerradura
Unión
Teorema de Kleen
Un lenguaje $L$ sobre el alfabeto $\Sigma$ es regular si y sólo si existe un AF con un alfabeto $\Sigma$ que acepta $L$
Una pausa
Vamos a repetirlo
Teorema de Kleen
Un lenguaje $L$ sobre el alfabeto $\Sigma$ es regular si y sólo si existe un AF con un alfabeto $\Sigma$ que acepta $L$
Otra pausa
Un lenguaje $L$ sobre el alfabeto $\Sigma$ es regular si y sólo si existe un AF con un alfabeto $\Sigma$ que acepta $L$
¿Qué información recuerda la máquina?
El estado
Dado un lenguaje $L$ y $w \in \Sigma*$
Vamos a definir al lenguaje $L/w$ como:
$L/w=\{ z\in \Sigma^* | wz \in L \}$
Ejemplo: $L/a$ si le concatenamos $z=(ba^*ba^*)^*$
$L/w$ son todas las cadenas que concatenadas a diferentes $z$ llegan a un estado final
- $\delta^*(q_0,w_1z)$
- $\delta^*(q_0,w_2z)$
- $\delta^*(\delta^*(q_0,w_1),z)$
- $\delta^*(\delta^*(q_0,w_2),z)$
- Para que ambos sean iguales, $\delta^*(q_0,w_1)=\delta^*(q_0,w_2)$
Comparar $L/a$ con $L/a^*$, son la misma
Comparar $L/a$, $L/a^*$, $L/a^*ba^*b$ ,son la misma
- $L/a^*$
- $L/a^*ba^*b$
- $L/(a^*ba^*b)^*$
Concatenadas con $(ba^*ba^*)^*$ siempre llegan a $q_0$, no son diferenciables
¿Qué hay de $L/a^*b$?, concatenada con $(a^*ba^*)^*(ba^*ba^*)^*$
- $L/a^*b$
- $L/a^*b(a^*ba^*b)^*$
Concatenadas con $(a^*ba^*)^*(ba^*ba^*)^*$ siempre llegan a $q_0$, no son diferenciables
Sin embargo,
- $L/(a^*ba^*b)^*$, con $z= (ba^*ba^*)^*$
- $L/a^*b(a^*ba^*b)^*$, con $z=(a^*ba^*)^*$
Si son diferenciables porque son dos $z$ diferentes
¿Cuantos estados hay para un lenguaje $L$?
¿Cuantos conjuntos diferenciables hay?
Los estados dividen en conjutos las cadenas
- Lenguajes regulares
- Expresiones regulares
- Básicas
- Composición
- Autómatas finitos
- Estados
- Estado final
- Estados aceptores
- Función de transición
- Función de transición extendida
- Cadenas diferenciables

La máquina sin memoria by Ivan V. Meza Ruiz is licensed under a Creative Commons Reconocimiento 4.0 Internacional License.
Creado a partir de la obra en http://turing.iimas.unam.mx/~ivanvladimir/slides/lfya/fsm.html.