Abro paréntesis, abro paréntesis, cierro paréntesis, ...

No lata, no: la totalidad arada dilato talón a talón— Juan Filloy

Ivan Meza

Para los lenguajes regulares

Jerarquía de Chomsky

Jerarquía de Chomsky

Hace dos semanas

Hoy después de la revisión uno

Protocolos de comunicación

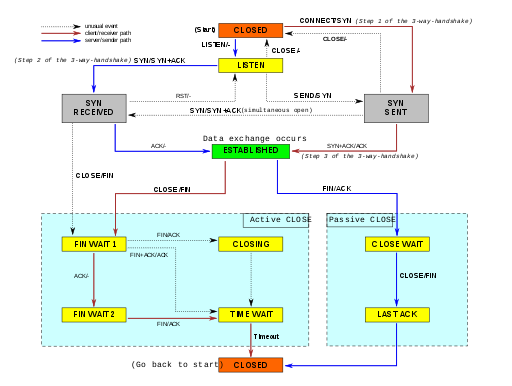
Extraido de aquí

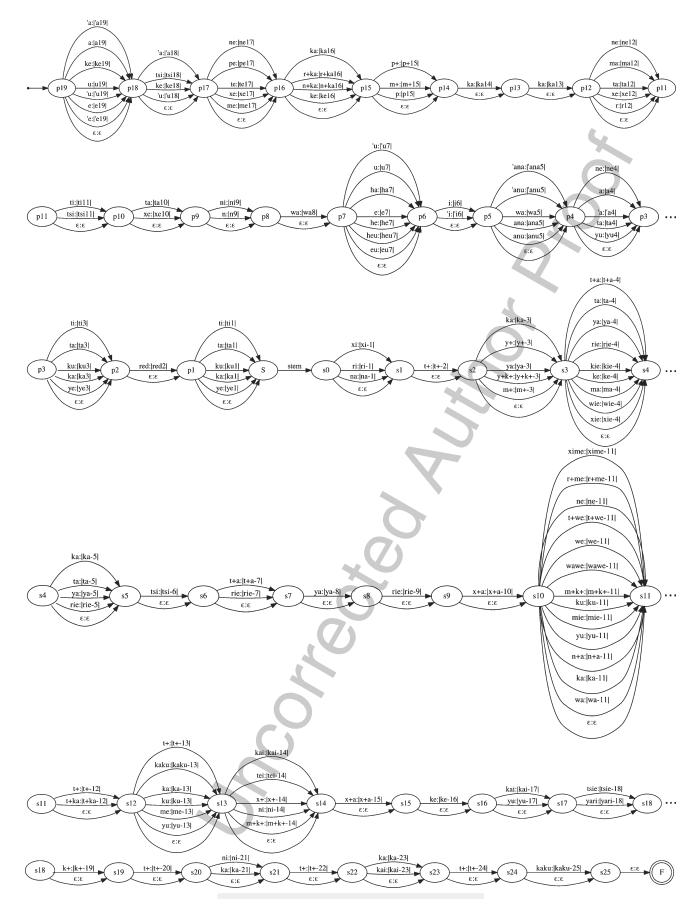
Verificación de URLS

Extraido de aquí, más discusión aquí

Morfología

Chatbots

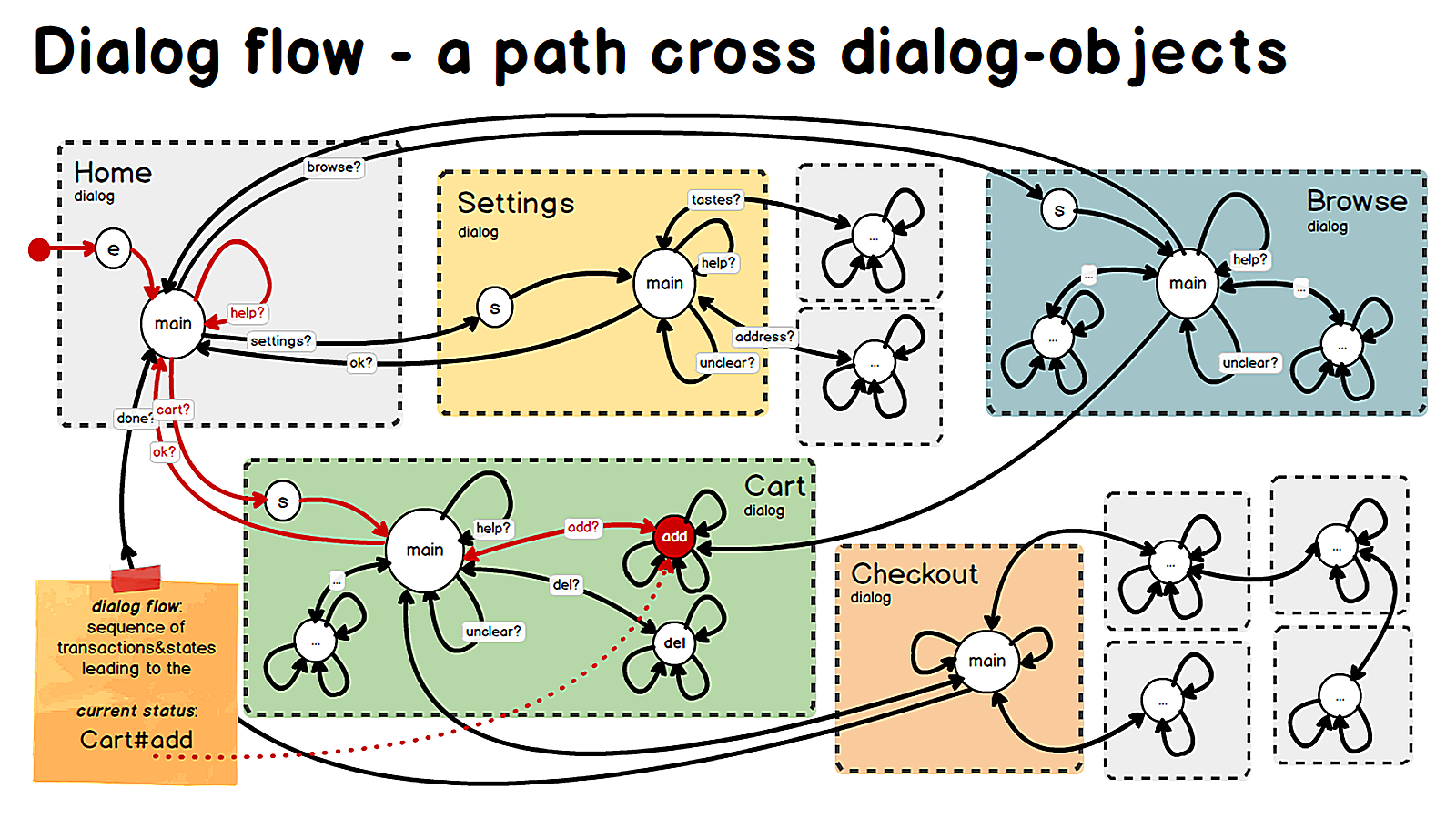
Extraido de aquí

Juegos

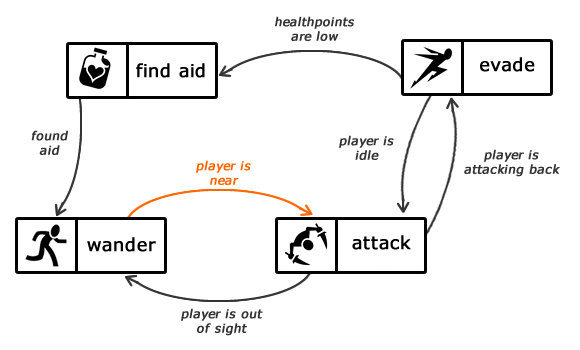
Extraido de aquí

Jerarquía de Chomsky

Lenguajes no regulares

Tipos de lenguajes

• Finitos: siempre son regulares
• Infinitos no siempre son regulares

AF en un lenguaje infinito

Para un $\Sigma$ y para $w \in L_R$

El trabajo del AF es circular $w$ por un conjunto finito de estados ($n$)

• ¿Qué podemos decir si $|w|$ es menor de $n$?
• ¿Qué podemos decir si $|w|$ es mayor o igual $n$?

El caso interesante

Para $w \in L_R$ y $|w| \ge n$

• Por lo menos un estado se repite
• La cadena se puede particionar en: $xyz$
• En donde $|xy|\le k$
• $x$ es un prefijo
• $y$ es un ciclo con $|y|\gt 1$
• $z$ es un sufijo

El ciclo

Para $w \in L_R$, $|w| \ge n$ y $w=xyz$

• Entonces $xy^kz \in L_R$

Ejemplo

• Proponer lenguaje, qué tal $\Sigma=\{a,b\}$ número par de bes
• Escoger $n$, qué tal $n$
• Proponer una cadena que dependa de $n$, qué tal $a^nbb$
• Particionar $w$, qué tal $x=a^{(n-1)}$, $y=a$, $z=bb$
• Checar que se cumplan restricciones, $|xy| \le n$, $y \not = \epsilon$
• Checar si $xy^kz \in L$ , sí pertenece $a^{(n-1)}a^kbb\in L$

No tan rápido, faltan más formas de cadenas en el lenguaje

Ejemplo (cont.)

Por ejemplo $n$ $(bb)^n$

• Particionar $w$, qué tal $x=b^{(n-2)}$, $y=bb$, $z=b^n$
• Checar que se cumplan restricciones, qué tal $|xy| \le n$, $y \not = \epsilon$
• Checar si $xy^kz \in L$, sí pertenece $b^{(n-2)}(bb)^kbb^n\in L$, ya que total de bes es $2k+2n-2$, que es par

No tan rápido todavía, faltan más formas de cadenas en el lenguaje

Probar que un lenguaje es regular por este procedimiento es demasiado trabajo, muchas veces con encontrar una expresión regular o un autómata finito, es suficiente

¡Es más fácil probar que no lo es!

A este procedimiento se le conoce como lema de bombeo

Un nuevo lenguaje con el mismo alfabeto

El lenguaje de as seguidas del mismo número de bes

$a^ib^i$

Ejemplos $\epsilon$, $ab$, $aabb$, $aaabbb$

$a^ib^i$

• ¿De qué tamaño es el lenguaje?

• Proponer lenguaje, qué tal$\Sigma=\{a,b\}$ con $a^ib^i$
• Escoger $n$, qué tal $n=i$
• Proponer una cadena que dependa de $n$, qué tal $a^nb^n$
• Particionar $w$, qué tal $x=a^{(n-1)}$, $y=a$, $z=b^n$
• Checar que se cumplan restricciones, $|xy| \le n$, $y \not = \epsilon$
• Checar si $xy^kz \in L$, no pertenece para cualquier $k$ $a^{(n-1)}a^kb^n\not\in L$, ya que sólo se cumple para $k=1$

Otra forma de verlo

¿Qué necesita recordar mi autómata?

Si tiene número par o impar de bes

¿Qué necesito recordar para $a^ib^i$?

Hay lenguajes que no son regulares

Vamos a presentar otra dimensión

Gramáticas

No confundir

Gramáticas libres de contexto

• $V$ es otro alfabeto que denominamos símbolos no terminales (generalmente en mayúsculas)
• $\Sigma$ es un alfabeto que denominamos símbolos terminales
• $P$ es conjunto de reglas con la forma $A\rightarrow \alpha$ donde $\alpha \in (\Sigma\cup V)^*$ y $A\in V$
• $S\in V$ que denominamos símbolo inicial

Producciones/Reglas

Para $a^ib^i$, $G=(\{S\},\{a,b\},P,S )$ donde $P$

• $S\rightarrow aSb$
• $S\rightarrow \epsilon$

Como proceso de reescritura

• $\underline{S}$
El subrayado sólo marca que elemento se está re-escribiendo
• $\Rightarrow a\underline{S}b$
• $\Rightarrow a\ a \underline{S}b\ b$
• $\Rightarrow a\ a\ a\underline{S}b\ b\ b$
• $\Rightarrow a\ a\ a\ \epsilon\ b\ b\ b$
• $\Rightarrow aaabbb$

Una derivación

Uno más bonito

$G=(\{R,B\},\{a,b,\epsilon,\emptyset\},P,R,+,*,(,) )$ donde $P$

• $R\rightarrow B$
• $R\rightarrow R+R$
• $R\rightarrow R^*$
• $R\rightarrow RR$
• $R\rightarrow (R)$
• $B\rightarrow a$
• $B\rightarrow b$
• $B\rightarrow \epsilon$
• $B\rightarrow \emptyset$

• $\underline{R}$
• $\Rightarrow \underline{R}^* $
• $\Rightarrow (\underline{R})^* $
• $\Rightarrow (\underline{R} R)^*$
• $\Rightarrow (\underline{R} R R)^*$
• $\Rightarrow (\underline{R} R R R)^*$
• $\Rightarrow (\underline{R} R R R R)^*$
• $\Rightarrow (R^* R \underline{R} R R)^*$

• $\Rightarrow (R^* R \underline{R} R R)^*$
• $\Rightarrow (R^* R R^* R \underline{R})^*$
• $\Rightarrow (\underline{R}^* R R^* R R^*)^*$
• $\Rightarrow (B^* \underline{R} R^* R R^*)^*$
• $\Rightarrow (B^* B \underline{R}^* R R^*)^*$
• $\Rightarrow (B^* B B^* \underline{R} R^*)^*$
• $\Rightarrow (B^* B B^* B \underline{R}^*)^*$
• $\Rightarrow (\underline{B}^* B B^* B B^*)^*$

• $\Rightarrow (\underline{B}^* B B^* B B^*)^*$
• $\Rightarrow (a^* \underline{B} B^* B B^*)^*$
• $\Rightarrow (a^* b \underline{B}^* B B^*)^*$
• $\Rightarrow (a^* b a^* \underline{B} B^*)^*$
• $\Rightarrow (a^* b a^* b \underline{B}^*)^*$
• $\Rightarrow (a^* b a^* b a^*)^*$

Un ejemplo más pequeño

• $\underline{R}$ $\Rightarrow \underline{R} + R$ $\Rightarrow \underline{B} + R$ $\Rightarrow a + \underline{R}$ $\Rightarrow a + \underline{B}$ $\Rightarrow a + b$
• $\underline{R}$ $\Rightarrow R + \underline{R}$ $\Rightarrow R + \underline{B}$ $\Rightarrow \underline{R} + b$ $\Rightarrow \underline{B} + b$ $\Rightarrow a + b$

Derivaciones por la izquierda y por la derecha

Un ejemplo más largo

En lenguaje aceptado por una gramática L(G)

Con $G=(V,\Sigma,P,S)$

$L(G)=\{w\in \Sigma^* | S \Rightarrow^* w\}$

Árboles

Otra forma de representar las derivaciones

$aaabbb$

$(a^*ba^*ba^*)^*$

$aaaaa$

• Lema de bombeo: Lenguajes que no son regulares
• Gramáticas Libres de Contexto
• Derivación
• Árboles