Recapitulación
Computer Science is no more about computers than astronomy is about telescopes— Edsger W. Dijkstra
Hace cuatro meses
- ¿Qué parte de la computación les gusta?
- ¿Cúal es su trabajo ideal al terminar la carrera?
- ¿En veinte años como crean que sea la computación?
- ¿En cincueta años?
Ahora sabemos cosas que no cambiarán
Lenguajes Formales y Autómatas
LFyA
Una marco teórico matemático-computacional
Alan M. Turing

Comenzamos con conceptos básicos
Símbolos básicos

Cadenas

Lenguajes

Nuestra misión durante el curso
Máquinas

| $L_{Rec}$ | Tipo 0 ($\alpha \rightarrow \beta$) | MT, APDo, AC | $L_n$,$L_\bar{f}$ |
| $L_{DC}$ | Tipo 1 ($\alpha V \beta \rightarrow \alpha \gamma \beta$) | Autómata lineal con fronteras | $ww, a^nb^nc^n$ |
| $L_{LC}$ | Tipo 2 ($V\rightarrow \alpha$) | Autómata de pila | $ww^r, a^nb^n$ |
| $L_{reg}$ | Tipo 3 ($V \rightarrow aA|\epsilon$) |
Autómata finito | $w, a^*$ |


Autómata finito
Es una tupla $(Q,\Sigma,q_0,A,\delta)$
- $Q$ conjunto finito de estados
- $\Sigma$ un alfabeto
- $q_0$ estado inicial
- $A$ estados finales
- $\delta$ función de transición $Q x A \rightarrow Q$
AF vs AFND vs AFND-$\epsilon$
Los tres son una tupla $(Q,\Sigma,q_0,A,\delta)$
| AF | AFND | AFND-$\epsilon$ |
|---|---|---|
| $Q$ | $Q$ | $Q$ |
| $\Sigma$ | $\Sigma$ | $\Sigma$ |
| $q_0 \in Q$ | $q_0 \in Q$ | $q_0 \in Q$ |
| $A \subseteq Q$ | $A \subseteq Q$ | $A \subseteq Q$ |
| $\delta: Q \times \Sigma \rightarrow Q$ | $\delta: Q \times \Sigma \rightarrow 2^Q$ | $\delta: Q \times (\Sigma \cup \{\epsilon\}) \rightarrow 2^Q$ |
Autómata de pila
Es una tupla $(Q,\Sigma,\Gamma,q_0,Z_0,A,\delta)$
- $Q$ conjunto finito de estados
- $\Sigma$ alfabeto de cadenas reconocidas
- $\Gamma$ alfabeto de pila
- $q_0$ estado inicial
- $Z_0$ símbolo inicial de la pila
- $A$ estados finales
- $\delta$ función de transición $Q \times (\Sigma \cup \{\epsilon\}) \times \Gamma \rightarrow Q\times\Gamma^*$

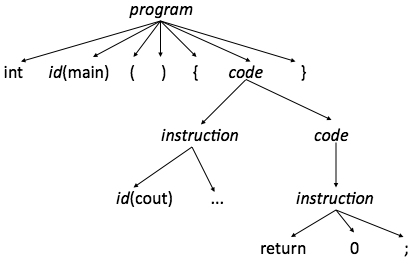
Autómata de pila determinístico (APD)
Es una tupla $(Q,\Sigma,\Gamma,q_0,Z_0,A,\delta)$
- Para cada $\delta(q,a,x)$ solo hay una trancisión
- Si $\delta(q,\epsilon,x)\ne \emptyset$, entonces $\delta(q,a,x)=\emptyset$
Gramáticas

veo al gato con el telescopio
¿quien tiene el telescopio?

Autómata de doble pila*
Es una tupla $(Q,\Sigma,\Gamma,q_0,Z_0,A,\delta)$
- $Q$ conjunto finito de estados
- $\Sigma$ alfabeto de cadenas reconocidas
- $\Gamma$ alfabeto de pila
- $q_0$ estado inicial
- $q_0$ símbolo inicial de la pila
- $A$ estados finales
- $\delta$ función de transición $Q \times (\Sigma \cup \{\epsilon\}) \times \Gamma \times \Gamma \rightarrow Q\times\Gamma^*\times\Gamma^*$
Un AFND-$\epsilon$ + dos pila
AP vs APD vs APDo
$(Q,\Sigma,\Gamma,q_0,Z_0,A,\delta)$
| AP | APD | APDo |
|---|---|---|
| $\delta: Q \times (\Sigma \cup \{\epsilon\}) \times \Gamma $ $\rightarrow Q\times\Gamma^*$ | $\delta: Q \times (\Sigma \cup \{\epsilon\}) \times \Gamma $ $\rightarrow Q\times\Gamma^*$ | $\delta:Q \times (\Sigma \cup \{\epsilon\}) \times \Gamma \times \Gamma$ $\rightarrow Q\times\Gamma^*\times\Gamma^*$ |
|
||
Recuerden que APD es tan poderosa como MT

Máquinas de Turing
Es una tupla $(Q,\Sigma,\Gamma,q_0,B,A,\delta)$
- $Q$ conjunto finito de estados
- $\Sigma$ alfabeto de cadenas reconocidas
- $\Gamma $ alfabeto de cinta, $\Sigma \subset \Gamma$
- $q_0$ estado inicial
- $B$ Símbolo de espacio en blanco $B \in \Gamma$ pero $B \not\in \Sigma$
- $A$ estados finales
- $\delta$ función de transición $Q \times \Gamma \rightarrow Q\times\Gamma\times\{der,izq\}$
Autómata lineal con frontera
Es una tupla $(Q,\Sigma,\Gamma,q_0,B,A,\delta)$
- $Q$ conjunto finito de estados
- $\Sigma$ alfabeto de cadenas reconocidas
- $\Gamma $ alfabeto de cinta, $\Sigma \subset \Gamma$
- $q_0$ estado inicial
- $B$ Símbolo de espacio en blanco $B \in \Gamma$ pero $B \not\in \Sigma$
- $A$ estados finales
- $\delta$ función de transición $Q \times \Gamma\cup \{\lt,\gt\} \rightarrow Q\times\Gamma\cup \{\lt,\gt\}\times\{der,izq\}$
Restricción, no se puede ir más allá de los símbolos $\lt,\gt$
ALF vs MT
| ALF | MT |
|---|---|
| $\delta: Q \times \Gamma\cup \{\lt,\gt\} $ $\rightarrow Q\times\Gamma\cup \{\lt,\gt\}\times\{der,izq\}$ | $\delta: Q \times \Gamma $ $\rightarrow Q\times\Gamma\times\{der,izq\}$ |
ALF es una MT con memoria restringida
Recuerden que ALF no es tan poderosa como MT

La tesis de Turing-Church
Toda computación efectiva puede llevarse a cabo por una máquina de Turing
Pero MT tambien nos trajo problemas
$L_{RE}$
Problemas indecidibles
$MT_U$

Garantiza que exista la industria del software
$L_{no\ RE}$
Problemas sin solución (sin máquinas de turing)
$L_{no\ RE} \rightarrow$ podemos checar que es una solución
$L_{co-RE} \rightarrow$ podemos checar que no es una solución
$REGULAR$

No magia
Pero también nos dejo un nuevo paisaje
| Más alla/No RE | -- | -- | $REGULAR$, $\overline{REGULAR}$, $L_{EQ}$ |
| co-RE/No RE | -- | -- | $\overline{L_u}$,$L_D$, $\overline{ONES}$, $ONLYONES$ |
| $L_{RE}/L_{Rec}$ | Tipo 0 ($\alpha \rightarrow \beta$) | MT, APDo, AC | $L_u$,$\overline{L_D}$, $ONES$, $\overline{ONLYONES}$/$L_n$,$L_\bar{f}$ |
| $L_{DC}$ | Tipo 1 ($\alpha V \beta \rightarrow \alpha \gamma \beta$) | Autómata lineal con fronteras | $ww, a^nb^nc^n$ |
| $L_{LC}$ | Tipo 2 ($V\rightarrow \alpha$) | Autómata de pila | $ww^r, a^nb^n$ |
| $L_{reg}$ | Tipo 3 ($V \rightarrow aA|\epsilon$) |
Autómata finito | $w, a^*$ |

Recapitulación by Ivan V. Meza Ruiz is licensed under a Creative Commons Reconocimiento 4.0 Internacional License.
Creado a partir de la obra en http://turing.iimas.unam.mx/~ivanvladimir/slides/lfya/recapit.html.