Regresión lineal y, sub y sobre ajuste

Ivan Meza

La metodología

$$\mathop{\textrm{argmin}}_\theta \sum_{i=i}^{n}E(f_\theta(x_i),y_i)$$

datos

Head Size and Brain Weight, R.J. Gladstone

La línea como un modelo

$$y=mx+b$$

Problema: estimar la línea a partir de los datos

Relación entre $x$ y $y$

Dada una $x$ identifico la $y$ resultante

Elementos de la línea

$$y=mx+b$$

$x$ variable independiente

$y$ variable dependiente

$m$ pendiente

$b$ intersección

Como modelo

$$f(x)=mx+b$$

Espacio de hipótesis

$\mathbb{H}=\{mx+b, \forall m\in \mathbb{R}, b\in \mathbb{R}\}$

Reformulando... (expandiendo \emph{x})

$$y=w_0x_0+w_1x_1 $$

$m=w_1$

$b=w_0$

$x=x_1$

$1=x_0$

¿... pero por qué...?

Como operación de matrices

$$ f(x)=W^TX= \begin{pmatrix} w_0 \\ w_1 \\ \end{pmatrix} \begin{pmatrix}x_0 & x_1\end{pmatrix} = \begin{pmatrix} w_0 \\ w_1 \\ \end{pmatrix} \begin{pmatrix}1 & x_1\end{pmatrix} $$

Pero podemos hacerlo mejor...

Pasando a $m$ dimensiones

$$ f(x)=W^TX= \begin{pmatrix} w_0 \\ w_1 \\ \vdots \\ w_m \\ \end{pmatrix} \begin{pmatrix}x_0 & x_1 & \cdots & x_m \end{pmatrix} =\\ \begin{pmatrix} w_0 \\ w_1 \\ \vdots \\ w_m \\ \end{pmatrix} \begin{pmatrix}1 & x_1 & \cdots & x_m \end{pmatrix} $$

Pero podemos hacerlo mejor...

Redefiniendo regresión lineal

Para un conjunto de $\boldsymbol{X}$ de $n$ datos en $\mathbb{R^m}$, de la forma $\boldsymbol{x}_{i=1}^n$ y para cual que agregamos un vector constante $x_{i0}=1$

Y para un conjunto de $y$ de $n$ puntos relacionados con $\boldsymbol{X}$ en posición.

Suponemos:

$f(\boldsymbol{x}_i)=W^T\boldsymbol{x}_i$

¿Qué dimensión tiene $W$?

Evaluación: Error cuadrado

$$ E(f(\boldsymbol{X}),y) = \frac{1}{2}\sum_{i=0}^n{(y_i - f(\boldsymbol{x}_i)^2)} $$

¿Qué agregué de forma tramposa?

Más específico

$$ E(f_W(\boldsymbol{X}),y) = \frac{1}{2}\sum_{i_0}^n (y_i - W^T\boldsymbol{x}_i)^2 $$

Mucho más específicos

$$ E(f_W(\boldsymbol{X}),y) = \frac{1}{2}\sum_{i=0}^n(y_i - \sum_{j=0}^m{w_j\boldsymbol{x}_{ij}})^2 $$

Optimización: búsqueda

$$ \mathop{\textrm{argmin}}_W \frac{1}{2}\sum_{i=0}^n(y_i - \sum_{j=0}^m{w_j\boldsymbol{x}_{ij}})^2 $$

Descenso por gradiente

Algunas funciones son fáciles

Tomado de Wikipedia

Algunas funciones son difíciles

Tomado de Wikipedia

Imaginemos

Recordemos

$$ E(f_W(\boldsymbol{X}),y) = \frac{1}{2}\sum_{i=0}^n(y_i - \sum_{j=0}^m{w_j\boldsymbol{x}_{ij}})^2 $$

Derivando para dimensión $d$

$$ \frac{dE(f_W(\boldsymbol{X}),y)}{dw_d}= \frac{d\frac{1}{2}\sum_{i=0}^n(y_i - \sum_{j=0}^m{w_j\boldsymbol{x}_{ij}})^2}{dw_d} $$

Derivadas de las sumas

$$ \frac{1}{2}\sum_{i=0}^n \frac{d(y_i - \sum_{j=0}^m{w_j\boldsymbol{x}_{ij}})^2}{dw_d} $$

Derivada de potencias

$$ \frac{1}{2} \sum_{i=0}^n 2 (y_i - \sum_{j=0}^m{w_j\boldsymbol{x}_{ij}})\frac{d (y_i - \sum_{j=0}^m{w_j\boldsymbol{x}_{ij}})}{dw_d} $$

Expandiendo sumatoria

$$ \frac{1}{2} \sum_{i=0}^n 2 (y_i - \sum_{j=0}^m{w_j\boldsymbol{x}_{ij}})\frac{d (y_i -w_0x_{0i} \ldots -w_dx_{di} \ldots -w_jx_{ji})}{dw_d} $$

Expandiendo sumatoria

$$ \frac{1}{2} \sum_{i=0}^n 2 (y_i - \sum_{j=0}^m{w_j\boldsymbol{x}_{ij}})\frac{d(-w_dx_{di})}{dw_d} $$

Derivando elementos

$$ \frac{1}{2} \sum_{i=0}^n 2 (y_i - \sum_{j=0}^m{w_j\boldsymbol{x}_{ij}}) (-x_{di}) $$

Simplificando

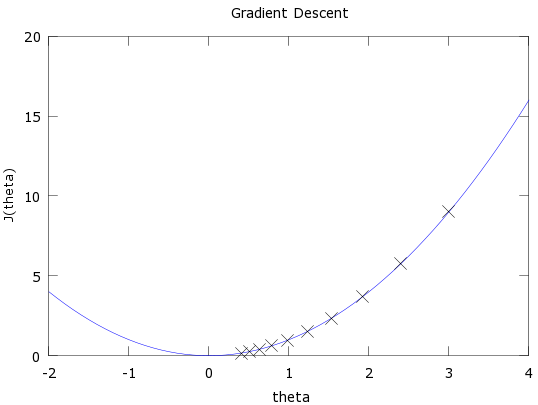
$$ \frac{dE(f_W(\boldsymbol{X}),y)}{dw_d}= \sum_{i=0}^n (y_i - f(\boldsymbol{x_i})) (-x_{di}) $$

$$\hat{w}_d= w_d - k \sum_{i=0}^n (y_i - f(\boldsymbol{x_i})) (-x_{di})$$

Tomado de Gradient Descent Derivation

Tomado de Wikipedia

¿Qué hay de $k$?

Tomado de CS231n

¿Pero con qué pesos comenzamos?

Aleatorio

Uniforme al número de pesos

Como es aproximativo, no siempre tenemos el mismo modelo

¿Que tipo de errores tenemos?

Podemos pensar que nuestro espacio de hipótesis $\mathbb{H}$ es un espacio de expertos

Cada experto tiene desarrolló una experiencia propia con el problema, entonces difieren en como resolver el problema

¿Que tipo de errores cometen?

Se equivocan siempre de igual forma

Se equivocan por todos lados

Es decir

El experto tiene un sesgo ($Bias$)

El experto tiene varianza ($Var$)

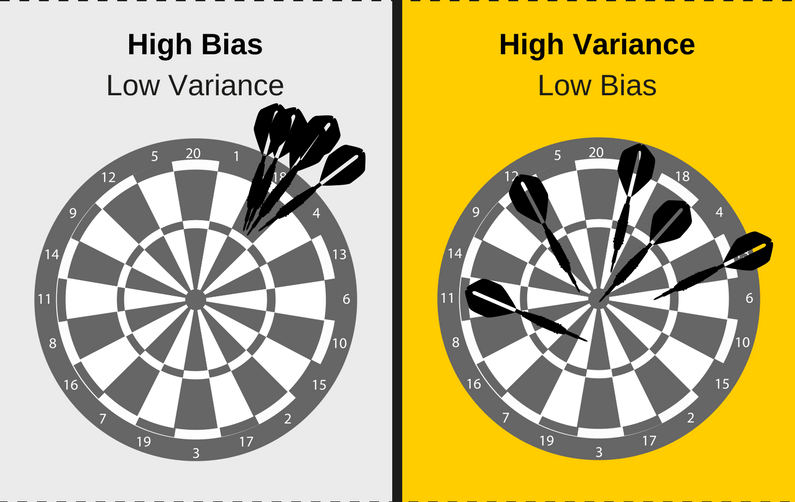
Tomado de WTF is the Bias-Variance Tradeoff?

Los errores son una combinación de ambos factores

Falta un tipo de error

Intrínsecos del problema ($\epsilon$)

¿Quien tiene la culpa del error?

¿El algoritmo o la hipótesis?

Valores esperados

Para variable discreta $$\mathbb{E}[X]=\sum_{i=0}^{n}x_ip(x_i)$$
Para distribución uniforme $$\mathbb{E}[X]=\frac{1}{n}\sum_{i=0}^{n}x_i$$

Predicción esperada

$$\mathbb{E}[f_\theta(x)]=\frac{1}{n}\sum_{i=0}^{n}f_\theta(\boldsymbol{x}_i)$$

Error cuadrático esperado

$$\mathbb{E}[(f_\theta(x)-y)^2]=\frac{1}{n}\sum_{i=0}^{n}(f_\theta(\boldsymbol{x}_i)-y)^2$$

Sesgo

Es la diferencie entre la predicción esperada y el valor verdadero

$$Bias[f_\theta(x)]=y-\mathbb{E}[(f_\theta(X)] $$

¿Por qué es malas noticias para nosotros?

Varianza

Es la diferencia entre la predicción al cuadrado esperada y el cuadrado de la predicción esperada

$$Var[f_\theta(x)]=\mathbb{E}[(f_\theta(X)^2]-\mathbb{E}[(f_\theta(X)]^2 $$

Error cuadrático esperado

$$\mathbb{E}[(f_\theta(x)-y)^2]=(y-\mathbb{E}[(f_\theta(X)])^2+\mathbb{E}[(f_\theta(X)^2]-\mathbb{E}[(f_\theta(X)]^2+\epsilon$$

O en otras palabras

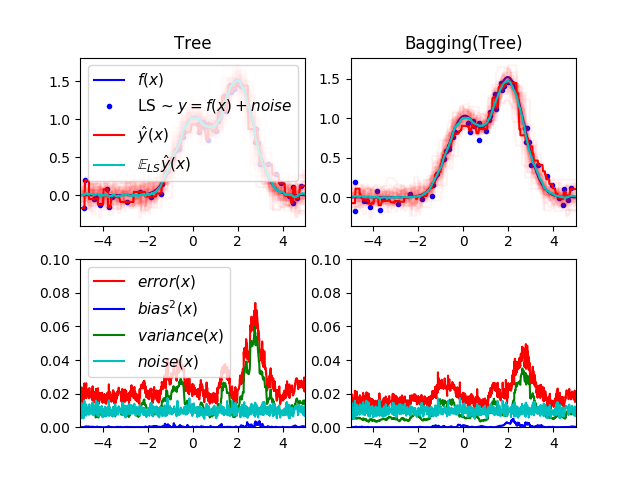
$$\mathbb{E}[(f_\theta(x)-y)^2]=Var[f_\theta(x)]+Bias[f_\theta(x)]^2+\epsilon$$

Tomado de Single estimator versus bagging: bias-variance decomposition

Compromiso entre sesgo y varianza

Modelos más sencillos, producen un alto sesgo

Modelos más complejos, producen un bajo sesgo

Modelos más sencillos, producen un baja varianza espacio $\mathbb{H}$ más grande

Modelos más complejos, producen un alta varianza espacio $\mathbb{H}$ más grande

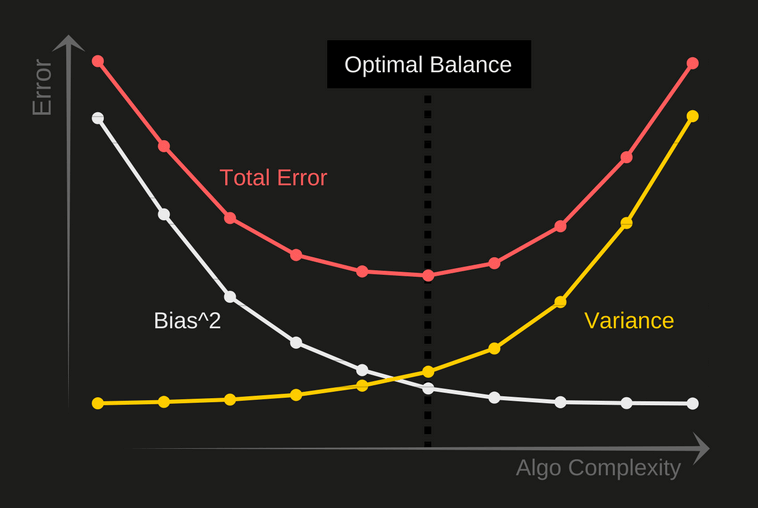
Tomado de WTF is the Bias-Variance Tradeoff?

Sub ajuste

Es cuando el modelo es muy simple que no es suficiente para modelar las relaciones de los datos de entrenamiento

Imaginen el modelo $y=c$

Sobre ajuste

Es cuando el modelo es muy complejo de tal forma que memoriza los datos de entrenamiento, lo único que modela es el ruido

Imaginen el modelo $f=g+\epsilon$

Ante nuevos datos falla más

Tomado de Underfitting vs. Overfitting

Regresión lineal y, sub y sobre ajusto by Ivan V. Meza Ruiz is licensed under a Creative Commons Reconocimiento 4.0 Internacional License.
Creado a partir de la obra en http://turing.iimas.unam.mx/~ivanvladimir/slides/rpyaa/02_regresión.html.