GNB, logistic regression, training

Ivan Meza

Naive Bayes discreta

$$ P(Y=y_k|X=x_1,\ldots,x_m) = \frac{\prod_{i}^{m}P(x_i|y)P(y)}{\sum_{k=0} \prod_{i}^{m}P(x_i|y_k)P(y_k)}$$

Naive Bayes clasificación

$$ \mathop{\textrm{argmax}}_{y_k} \prod_{i}^{m}P(x_i|y_k) $$

Parámetros

$$ P(x_i|y_k) = \frac{|\mathbb{D}{x_i \land y_k}|}{|\mathbb{D}{y_k}|}$$

¿Entradas continuas?

Tenemos que cambiar $p(X_i|Y)$, para modelar el comportamiento de $X_i$ dado una $Y$

Si $X_i$ es continuo, no es posible usar cuentas de su ocurrencia.

Una forma barata de representar la distribución Gaussiana

Distribución Gaussiana

$$\mathcal{N(x|\mu,\sigma)}=\frac{1}{\sqrt{2\pi\sigma^2}}\exp^{\frac{-(x-\mu)^2}{2\sigma^2}} $$

$\mu$ es la media de la Gaussiana, y $\sigma$ la desviación estándar

Parámetros

Dos parámetros por característica, por número de salidas posibles, es decir $2mk$ donde $m$ es el número de características, y $k$ el número de clases

$$\mu_{ij}=\mathbb{E}[X_i|y_j] $$
$$\sigma^2_{ij}=\mathbb{E}[(X_i-\mu_{ij})^2|y_j] $$

La media

$$\mu_{ij}=\frac{\sum_j X_i\delta(y_j,k) }{\sum_n\delta(y_j,k)}$$

Para una cantidad de $n$ datos podemos usar MLE

Donde $\delta$ es una función selector que regresa $1$ cuando el dato $k$ coincide con la clase $y_j$

La $\mu$ para la característica $i$ dada la clase $j$ es la suma de todos los valores $X_i$ dónde la salida fue la clase $y_j$

La desviación estándar

Para una cantidad de $n$ datos podemos usar MLE

$$\sigma^2_{ij}=\frac{\sum_j (X_i-\mu_{ij})^2\delta(y_j,k) }{\sum_n\delta(y_j,k)}$$

Sin embargo se prefiere el estimador mínimo sin varianza sin sesgo (MVUE, siglas en inglés)

$$\sigma^2_{ij}=\frac{\sum_j (X_i-\mu_{ij})^2\delta(y_j,k) }{\sum_n\delta(y_j,k)-1}$$

La $\sigma$ para la característica $i$ dada la clase $j$ es la suma de las diferencias al cuadrado del dato $X_i$ con $\mu_{ij}$ dónde la salida fue la clase $y_j$

Naive Bayes continua

$$ P(Y=y_j|X=x_1,\ldots,x_m) = \frac{\prod_{i}^{m}\mathcal{N}(x_i|\mu_{ij},\sigma_{ij})P(y_j)}{\sum_{k=0} \prod_{i}^{m}\mathcal{N}(x_i|\mu_{ij},\sigma_{ij})P(y_k)}$$

Naive Bayes continua clasificación

$$ \mathop{\textrm{argmax}}_{j} \prod_{i}^{m}\mathcal{N}(x_i|\mu_{ij},\sigma_{ij}) $$

¿Podemos usar un modelo como el de regresión lineal, para clasificar?

Función sigmoide logística

$$ S(x) = \frac{1}{1+e^{-x}}$$

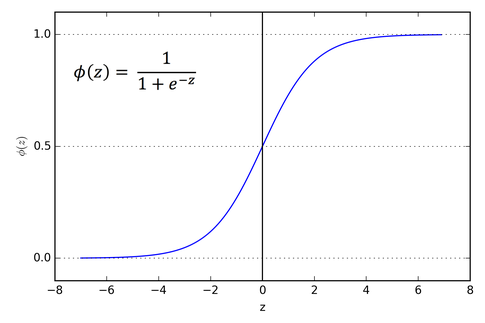
Clasificación con pesos

si $x=W^TX$ y $Y$ binaria

$$ S(W^TX) = \frac{1}{1+e^{W^TX}}$$
$$ S(W^TX) = \frac{1}{1+e^{-(w_0+w_1x_1+w_2x_2+\ldots+w_mx_m)}}$$
$$ S(W^TX) = \frac{1}{1+e^{-(w_0+\sum_{i=1}^m w_ix_i)}}$$

Ajustando los pesos

Una opción es hacerlo a través de la distribución Gaussiana

$$ P(1|X) =\frac{(X|1)P(1)}{P(X|1)P(1)+P(X|0)P(0)}$$

Si dividimos entre $P(X|1)P(1)$ al denominador y numerador

$$ P(1|X) =\frac{1}{1+\frac{P(0)P(X|0)}{P(1)P(X|1)}}$$

$$ P(1|X) =\frac{1}{1+\exp \left( \ln \frac{P(0)P(X|0)}{P(1)P(X|1)}\right)}$$

Si asumimos independencia entre las variables

\begin{align} P(1|X) & = \frac{1}{1+\exp \left( \ln \frac{P(0)}{P(1)}+\sum_i \ln \frac{P(X_i|0)}{P(X_i|1)}\right)}\\ & = \frac{1}{1+\exp \left( \ln \frac{1-\pi}{\pi}+\sum_i \ln \frac{P(X_i|0)}{P(X_i|1)}\right)}\\ \end{align}

Si asumimos $P(X_i|y)$ es una Gaussiana, y qué $\sigma_{i0}=\sigma_{i1}$

$$ \begin{align} \frac{P(X_i|0)}{P(X_i|1)} & = \sum_{i_1}^n \ln \left(\frac{ \frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( \frac{-(X_i-\mu_{i0})^2}{2\sigma^2_i } \right)} }{\frac{1}{\sqrt{2\pi\sigma^2}} \exp{\left( \frac{-(X_i-\mu_{i1})^2}{2\sigma^2_i } \right)}} \right) \\ & = \sum_{i_1}^n \ln \exp \left(\frac{(X_i-\mu_{i1})^2- (X_i-\mu_{i0})^2}{2\sigma^2_i } \right) \\ & = \sum_{i_1}^n \left(\frac{(X_i^2-2X_i\mu_{i1}+\mu_{i1}^2)- (X_i^2-2X_i\mu_{i0}+\mu_{10}^2)}{2\sigma^2_i } \right) \\ & = \sum_{i_1}^n \left(\frac{2X_i(\mu_{i0}-\mu_{i1})+\mu_{i1}^2-\mu_{i0}^2}{2\sigma^2_i } \right) \\ & = \sum_{i_1}^n \left(X_i\frac{\mu_{i0}-\mu_{i1}}{\sigma^2}+\frac{\mu_{i1}^2-\mu_{i0}^2}{2\sigma^2_i } \right) \\ \end{align} $$

Regresando

\begin{align} P(1|X) & = \frac{1}{1+\exp \left( \ln \frac{1-\pi}{\pi}+\sum_{i_1}^n \left(X_i\frac{\mu_{i0}-\mu_{i1}}{\sigma^2}+\frac{\mu_{i1}^2-\mu_{i0}^2}{2\sigma^2_i } \right) \right)}\\ & = \frac{1}{1+\exp \left( {w_0+\sum_{i=1}^m w_ix_i} \right) } \\ \end{align}

Acomodando

\begin{align} w_0 = \ln \frac{1-\pi}{\pi} + \sum_{i_1}^n \frac{\mu_{i1}^2-\mu_{i0}^2}{2\sigma^2} \end{align}

\begin{align} w_i = \sum_{i}^n \frac{\mu_{i1}-\mu_{i0}}{\sigma^2} \end{align}

Estos pesos son los que concuerdan con GNB (asumimos distribución gaussiana e independencia)

¿Qué tal si no queremos asumir GNB?

En el marco probabilístico buscamos maximizar la probabilidad asignadas a la clasificación, es decir el likehood condicional de los datos

$$ L(W) = \prod_i^n P(Y_i|X_i,W) $$

Entre más grande la probabilidad asignada, el producto es más grande. Sin embargo, nos conviene trabajar con el $log$ likehood

$$ \mathcal{L}(W) = \sum_i^n \log P(Y_i|X_i,W) $$

Para una $Y$ binaria

$$ \mathcal{L}(W) = log \sum_i^n P(Y_i|X_i,W) $$

Entre más grande la probabilidad asignada, el producto es más grande. Sin embargo, nos conviene trabajar con el $log$ likehood

$$ \mathcal{L}(W) = log \sum_i^n P(Y_i|X_i,W) $$

Existen dos tipos de términos

\begin{align} \mathcal{L}(W) &= \sum_i^n \log Y_iP(1|X_i,W)+(1-Y_i)\log P(0|X_i,W) \\ \end{align}

Fijarse que $Y$ se usa para apagar y prender los términos dependiendo si es $0$ o $1$

\begin{align} \mathcal{L}(W) & = \sum_i^n Y_i\log P(1|X_i,W)+\log P(0|X_i,W)-Y_i\log P(0|X_i,W) \\ & = \sum_i^n Y_i\log \frac{P(1|X_i,W)}{P(0|X_i,W)}+\log P(0|X_i,W) \\ \end{align}

$$ P(0|X,W) = \frac{1}{1+exp^{w_0+\sum_{i=1}^m w_ix_i}}$$

entonces

$$ P(1|X,W) = 1-P(0|X,W) = \frac{\exp^{w_0+\sum_{i=1}^m w_ix_i}}{1+\exp^{w_0+\sum_{i=1}^m w_ix_i}}$$

Remplazando

\begin{align} \mathcal{L}(W) & = \sum_i^n Y_i (w_0+\sum_j^m W_jx_j) - \log (1+ \exp(w_0+\sum_j^m W_jx_j)) \\ \end{align}

Que no tiene forma cerrada. Como queremos maximizar, usaremos Gradient Ascent

Actualización de pesos

$$ \hat{w_j} = w_j + k \sum_i^n x_{ij}\left( y_i - \frac{\exp{\sum_{k=0}^m w_k x_k}}{1+\exp{\sum_{k=0}^m w_k x_k}} \right) \\ $$

Con regularización $l2$

$$ \hat{w_j} = w_j + k \sum_i^n x_{ij}\left( y_i - \frac{\exp{\sum_{k=0}^m w_k x_k}}{1+\exp{\sum_{k=0}^m w_k x_k}}\right) -k\alpha w_i \\ $$

Cuando no se cumple GNB, entonces LR y GNB aprenden diferentes funciones, pero en datos infinitos ambos convergen.

Metodología general

Problemas

Errores: sesgo + varianza + error
Subajuste: modelo muy sencillo
Sobreajuste: modelo muy complejo

No muy prometedor

¿Qué tan bueno es nuestro modelo/sistema?

Poder predictivo

Marco general

$f: X \rightarrow y$

En el caso supervisado, quiere decir que tengo $n$ ejemplos (datos) $(X,y)$

Vamos a esconderle unos datos a nuestro modelo, y vemos como se desempeña con ellos

Comparo las predicciones $y'$ de estos datos, con las que debió haber dado $y$

Datos

Entrenamiento datos que uso para calcular parámetros del modelo

Prueba datos que uso para comparar predicciones del modelo con lo que debería dar

Pecado capital

Nunca uso datos de entrenamiento para cuantificar el desempeño de mi modelo

!Nunca!

De hecho...

No veo nada sobre mis datos de prueba, ni siquiera las salidas del sistema

!Nada!

Pero es muy informativo ver las salidas de las predicciones

Datos desarrollo

Desarrollo datos que uso para ganar intuición de qué está bien o mal con el modelo

Tipos de datos

Entrenamiento
Desarrollo
Prueba

¿De dónde salen?

Algunos problemas que estudiamos ya tienen está división

train, dev y test

o train y test

Dilema

Más datos, mejor parámetros

Los datos supervisados son caros

¡Ni modos! la certeza del desempeño es más valiosa

Kaggle

Sitio de competencias, nos dan datos de entrenamiento; semanas después nos dan datos de prueba, los predecimos les entregamos nuestras predicciones y nos evaluan

Otros casos

Nosotros decidimos, la cantidad de datos es un factor

Suficientes
Pocos

Suficientes

Nosotros hacemos la partición

Suficientes: 60%, 20%, 20%
Muchos: 80%, 10%, 10%
Demasiados: 90%, 5%, 5%

Pocos

Validación cruzada: $k$-fold
Validación cruzada: One-left-out
Bootstraping: muestreo con remplazo

¿Qué hay de la evaluación?

	Positivo	Negativo
Positivo'	Verdadero positivo (TP)	Falso positivo (FP)
Negativo'	Falso negativo (FN)	Verdadero negativo (TN)

Accuracy

$$ \frac{TP+TN}{TP+TN+FP+FN} $$

De los que dije, cuales dije bien

Precisión

Positive predictive value

$$ \frac{TP}{TP+FP} $$

De los que dije positivo, cuales realmente eran positivos

Covertura (recall)

True positive rate, sensicibilidad

$$ \frac{TP}{TP+FN} $$

Cuantos positivos dije de los que debi haber dicho

Especificidad

$$ \frac{TN}{TN+FP} $$

Cuantos negativos dije de los que debi haber dicho

FPR

False positive rate

$$ \frac{FP}{FN+TN} $$

Cuantos negativos no dije, de todos los que dije

F-score

$$ \frac{2 \cdot precision \cdot recall}{precision + recall} $$

Cuantos negativos dije de los que debi haber dicho

Curva ROC

Grafico FPR contra Recall para distintos umbrales de decisión de positivo

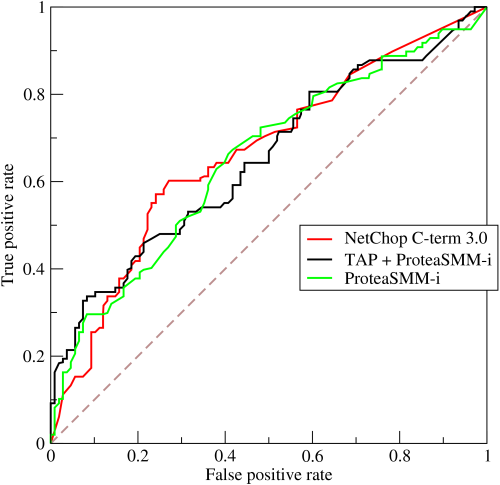
Curva ROC

Muestra el comportamiento cuando el umbral crece

Sistema ideal, al

Área bajo la curva (AUC)

Área bajo una curva ROC

Regresión lineal y, sub y sobre ajusto by Ivan V. Meza Ruiz is licensed under a Creative Commons Reconocimiento 4.0 Internacional License.
Creado a partir de la obra en http://turing.iimas.unam.mx/~ivanvladimir/slides/rpyaa/02_regresión.html.