Máquinas de soporte vectorial
Repensando el problema de clasificación
- Naïve Bayes $P(Y|X)$
- Sigmoide logistica $Y=S(\alpha_0x_0+\alpha_1x_1\cdots\alpha_mx_m)$
- Árbol de decisión $Y=T(X)$
- Bosqué aleatorio $Y=T_0(X)\oplus T_1(X)\oplus \cdots \oplus T_m(X)$
Separar con hyperplano
El problema con separación por hyperplano
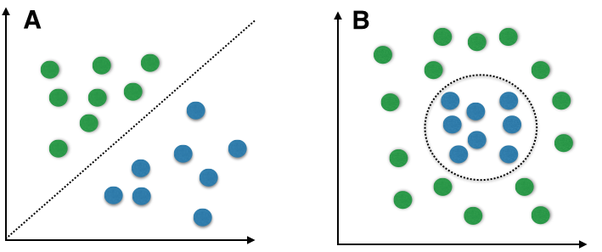
No todo es separable, posponemos el problema
¿Por qué hyperplano?
Generalización
- 1D es un punto
- 2D es una línea
- 3D es una plano
- 4D y más es un hyperplano y
Muchas líneas
... digo hyperplanos
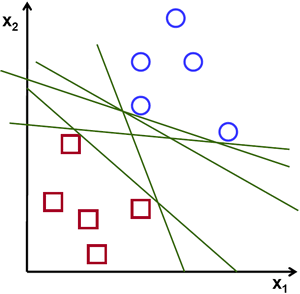
Margen
Ni tanto que queme al santo, ni tanto que no lo alumbre
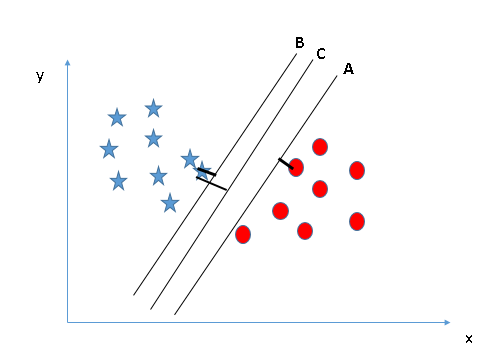
La línea con el margen máximo
... digo el hyperplano
El hyperplano
$$ w^Tx+b=0 $$Distancia a un punto
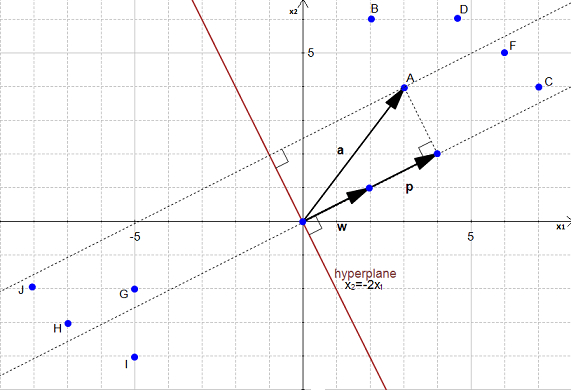 $$ p = (u \cdot a)u; u=\frac{w}{|w|} $$
$$ p = (u \cdot a)u; u=\frac{w}{|w|} $$
Pero...
El calculado no el más adecuado
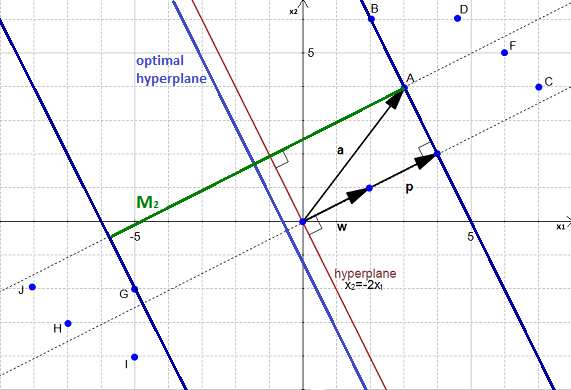
¿Cómo?
Fácil
- Conseguir ejemplos, dataset
- Seleccionar dos hyperplanos que no tengan puntos enmedio
- Maximizar su distancia, margen
Clasificación binaria
$$\mathbb{D}=(X,\{-1,+1\})$$Necesitamos dos hyperplanos que separen los datos: $$\begin{align} H_2: & W^Tx+b=\delta\\ H_3: & W^Tx-b=-\delta \end{align} $$
Simplificando
$$\begin{align} H_2: & W^Tx+b=1\\ H_3: & W^Tx-b=-1 \end{align} $$Para nuestros datos
$$\begin{align} W^Tx_i+b \geq 1 & \text{ para todos los puntos de clase } +1\\ W^Tx_i+b \leq 1 & \text{ para todos los puntos de clase } -1\\ \end{align} $$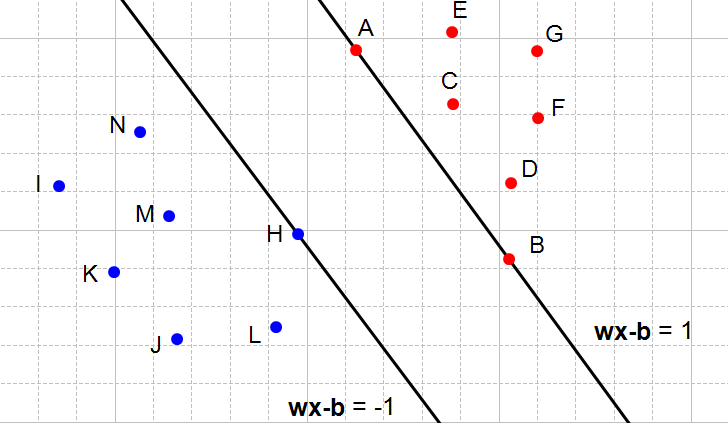
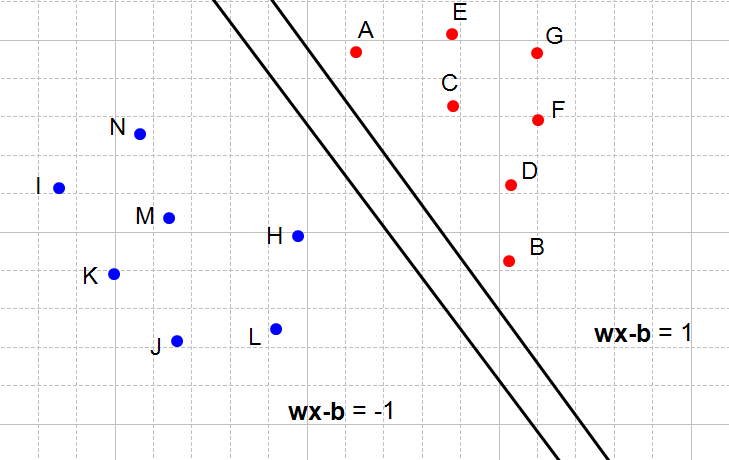
Combinando restricciones
$$ y_i(W^Tx_i+b) \geq 1 \text{ para todos los puntos} $$Sólo queda hacer máximo el márgen
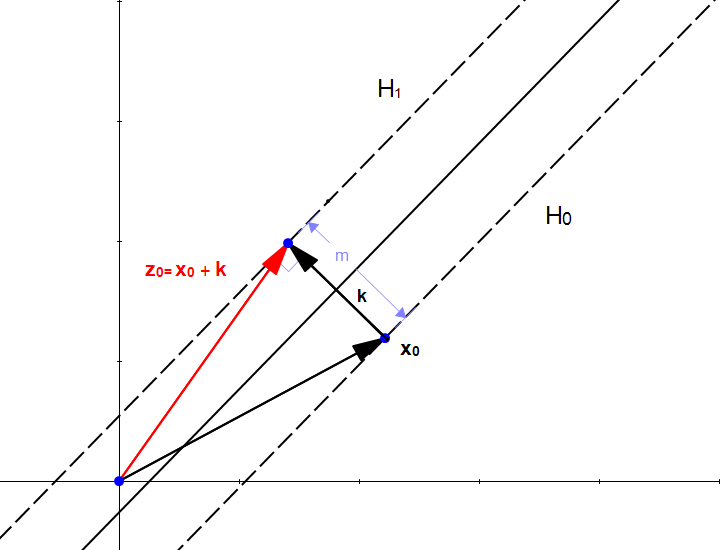 $$ m=\frac{2}{|w|} $$
$$ m=\frac{2}{|w|} $$
Maximizar es minimizar
Maximizar el margen $m$ es minimizar la norma de $w$, $|w|$
Problema de optimización
$$ \begin{align} \mathop{\textrm{min}}_{w,b} & |w| \\ \textrm{sujeto a } & y_i(W^Tx_i+b) \geq 1 \end{align} $$Preparando para la armada
$$ \begin{align} \mathop{\textrm{min}}_{w,b} & \frac{1}{2}|w|^2 \\ \textrm{sujeto a } & 1- y_i(W^Tx_i+b) \leq 0 \end{align} $$Función convexa
Lagrangianos
$$ \mathcal{L}(w,b,\lambda) = \frac{1}{2}|w|^2 -\sum_{i=0}^n \lambda_i (y_i(W^Tx_i+b)-1) $$Después de unas horas...
$$ \mathcal{L}(w,b,\lambda) = \sum_{i=1}^n\lambda_i - \frac{1}{2}\sum_{i=0}^n \sum_{j=0}^n \lambda_i\lambda_jy_iy_jx_i^Tx_j $$Sujetos a
$$\begin{align} \lambda_i \geq & 0\\ \sum_{i=0}^n \lambda_iy_i= & 0 \end{align} $$Finalmente
$$f(X)=W^T+b $$Donde
Sujetos a
$$\begin{align} w = & \sum_{i:S}\lambda_iy_ix_i\\ b = & \frac{1}{p}\sum_{i:S} \left(y_i -\sum_{j_i}^n \lambda_jy_jx_j^Tx_j \right)\\ \end{align} $$No tan rápido
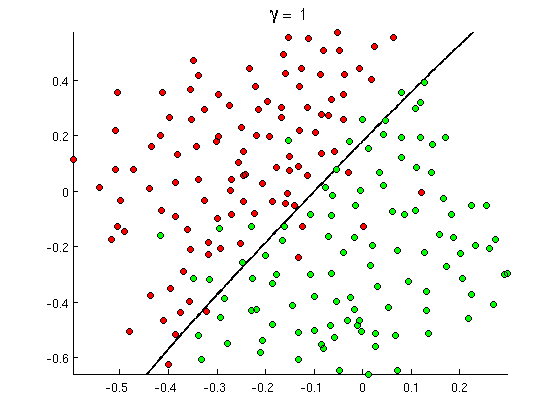
Variables slack
$$ \begin{align} \mathop{\textrm{min}}_{w,b,\xi} & \frac{1}{2}|w|^2 \\ \textrm{sujeto a } & y_i(W^Tx_i+b) \geq (1-\xi_i)\\ & \xi_i \geq 0\\ & \sum_{i=0}^n \xi_i \leq \mathbf{C} \end{align} $$Las variables $\xi$ nos dicen si el punto puede estar dentro del margen, relajan por punto su relación con el margen
El problema con separación por hyperplano

Regresando al problema
El truco de kernel
¿Cómo capturar la no linealidad?
Hacer expansión dimensional
Por ejemplo: expansión polinomial para dos dimensiones
- $(x_1,x_2)\rightarrow x_1,x_2,x_1^2,x_2^2,x_1x_2$
O, sigmoide
- $(x_1,x_2)\rightarrow tanh(w_{11}x_1+w_{12}x_2+w_{213})+tanh(w_{21}x_1+w_{22})$
Problemas con expansión
- El número de dimensiones crece mucho
- Polinomial $O(n^k)$
- Sobre ajuste, aquí el margen ayuda
Recordemos sin valiables slack
$$ \mathcal{L}(w,b,\lambda) = \sum_{i=1}^n\lambda_i - \frac{1}{2}\sum_{i=0}^n \sum_{j=0}^n \lambda_i\lambda_jy_iy_jx_i^Tx_j $$Sujetos a
$$\begin{align} \lambda_i \geq & 0\\ \sum_{i=0}^n \lambda_iy_i= & 0 \end{align} $$Re-escribiendo xs
$$ \mathcal{L}(w,b,\lambda) = \sum_{i=1}^n\lambda_i - \frac{1}{2}\sum_{i=0}^n \sum_{j=0}^n \lambda_i\lambda_jy_iy_j(x_i\cdot x_j) $$Sujetos a
$$\begin{align} \lambda_i \geq & 0\\ \sum_{i=0}^n \lambda_iy_i= & 0 \end{align} $$Sólo tenemos que transformar el producto $x_i\cdot x_j$, no es necesario saber todas las dimensiones
Función kernel
No vamos a mapear todos los puntos, sino solamente sus productos puntos
$$ K(x_i,x_j)=g'(x_i)\cdot g'(x_j) $$No necesitamos saber $g'$ sino sólo $K$
Ejemplos
$$ \begin{align} K(x_i,x_j) = & (x_i\cdot x_j +1 )^p & \text{Polonimial} \\ K(x_i,x_j) = & exp^{\frac{|x_i-x_j|^2}{2\sigma^2}} & \text{RBF gausianas} \\ K(x_i,x_j) = & tanh(wx_i\cdot x_j-\delta) & \text{Sigmoide} \\ \end{align} $$
Tomado de documentación sklearn
Aplicaciones
- Clasificación de imágenes
- Clasificación de textos
- Reconocimiento de voz
- Bioinformática
Clasificación de imágenes
Varias tareas
- Clasificación de dígitos
- Identificación de rostros
- Clasificación de objetos
Extracción de características
Convertir imágenes representación vectorial, visión por computadora
- Vectores sift
- Filtros en cascadas
- Filtros HOG
- Filtros Gabbor
Uso de histogramas de intensidades
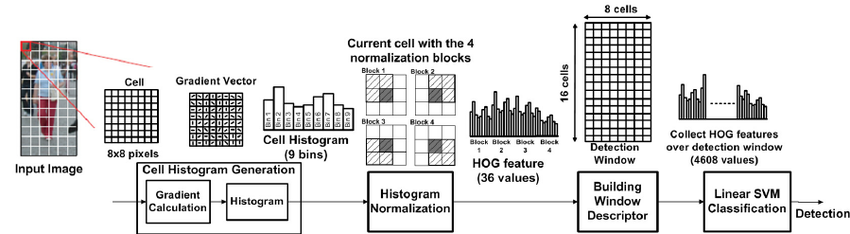
Basado es Energy-Efficient HOG-based Object Detection at 1080HD 60 fps with Multi-Scale Support
Clasificación de texto
Varias tareas
- Analisis de sentimientos
- Clasificación de ironía
- POS tagging
Extracción de características
Convertir texto representación vectorial, procesamiento de lenguaje natural
- Vectores de frecuencias
- TDF-ID
- Vectores de características
Uso de histogramas de palabras
| Voca. | $t_i$ | $d_0$ | $d_1$ | $\ldots$ |
| el | $840$ | $4$ | $5$ | $\ldots$ |
| en | $220$ | $3$ | $1$ | $\ldots$ |
| perro | $10$ | $0$ | $3$ | $\ldots$ |
| gato | $8$ | $2$ | $1$ | $\ldots$ |
| vaso | $5$ | $0$ | $1$ | $\ldots$ |
Fórmula
Frecuency,
Term frecuency,
Inverse Document Frecuency

Regresión lineal y, sub y sobre ajusto by Ivan V. Meza Ruiz is licensed under a Creative Commons Reconocimiento 4.0 Internacional License.
Creado a partir de la obra en http://turing.iimas.unam.mx/~ivanvladimir/slides/rpyaa/02_regresión.html.