Lógica Computacional
Nota 02. Lógica proposicional

1 Introducción

La meta de la lógica en Ciencias de la Computación es desarrollar lenguajes que modelen las situaciones con las que nos encontramos como científicos de la computación, de tal modo que podamos razonar acerca de ellas formalmente, lo cual significa construir argumentos que las describan. Por ejemplo,

Ejemplo 1.1

Si un tren llega tarde y no hay taxis en la estación, entonces Juan llega tarde a su reunión. Juan no llega tarde a su reunión. El tren llegó tarde. Por lo tanto, hubo taxis en la estación.

Intuitivamente, el argumento es válido. Otro ejemplo:

Ejemplo 1.2

Si está lloviendo y Laura no tiene paraguas, entonces ella se mojará. Laura no está mojada. Está lloviendo. Por lo tanto, Laura tiene paraguas.

Este argumento también es válido. Veamos un ejemplo más:

Ejemplo 1.3

Si Rivendell es destruido y Chewbacca no es un saiyajin, entonces es amigo de Lex Luthor. Chewbaca no es amigo de Lex Luthor. Rivendell es destruido. Por lo tanto, Chewbacca es un saiyajin.

Un análisis cuidadoso revela que en realidad los tres ejemplos anteriores tienen la misma estructura, aunque el tercero carezca de significado.

El argumento en cada ejemplo pudo haberse presentado sin hablar de trenes o de lluvia, como sigue:

Si $p$ y no $q$, entonces $r$. No $r$. $p$. Por lo tanto, $q$.

En el desarrollo de la lógica, no nos interesa el significado real, sino sólo la estructura lógica.

2 Oraciones declarativas

Para lograr que los argumentos sean rigurosos, necesitamos desarrollar un lenguaje en el que podamos expresar oraciones de un modo que obtengamos su estructura lógica. Empezamos con el lenguaje de la lógica proposicional, el sistema lógico más simple. Se basa en proposiciones u oraciones declarativas que podemos clasificar como verdaderas o falsas. Por ejemplo:

1. La suma de los números 3 y 22 es 25.

2. Superman es más fuerte que Batman.

3. El uniforme de los Pumas es el más bonito de todos.

4. A todos los marcianos les gusta el pepperoni en sus pizzas.

Las cuales son capaces de ser declaradas ‘verdaderas’ o ‘falsas’. Las oraciones declarativas pueden efectuarse en cualquier lenguaje natural o artificial.

Ejemplos de oraciones no declarativas son:

• ¿Me pasas la sal, por favor?

• Que la fuerza te acompañe.

• ¿Cómo estás?

• ¡Felicidades!

• ¡Haz tu tarea!

Estamos interesados en oraciones declarativas precisas acerca del comportamiento de programas. No solo queremos especificar tales oraciones, queremos también verificar si tales programas satisfacen una especificación dada. Por lo que necesitamos desarrollar una teoría de razonamiento que nos permita llegar a conclusiones a partir de suposiciones y que preserve la verdad: si todas nuestras suposiciones son verdaderas, entonces nuestra conclusión también debe ser cierta.

La lógica que diseñaremos es simbólica. Traduciremos un conjunto de oraciones declarativas del español a cadenas de símbolos. Nuestra estrategia será considerar ciertas oraciones declarativas como atómicas.

Asignamos símbolos diferentes $p,q,r,\mathrm{\dots },p_1,q_1,r_1,\mathrm{\dots }$ a cada una de las oraciones atómicas, por lo que ahora podemos codificar oraciones más complejas. Dadas las oraciones atómicas:

$p$:	gané la lotería la semana pasada
$q$:	compré un boleto de lotería
$r$:	gané las apuestas de la semana pasada

podemos formar oraciones más complejas de acuerdo a las reglas siguientes:

$\neg p$:	No es cierto que gané la lotería la semana pasada.
$p\vee q$:	Establece que al menos uno de ellos es cierto. Gané la lotería la semana pasada o gané las apuestas de la semana pasada.
$p\wedge q$:	Establece que ambos tienen que ser ciertos. La semana pasada gané la lotería y las apuestas.
$p\to q$:	Sugiere que $q$ es consecuencia lógica de $p$. Si gané la lotería la semana pasada, entonces compré un boleto de lotería.

3 Sintaxis

La sintaxis de la lógica proposicional se anuncia a continuación.

Definición 3.1

Sintaxis de la lógica proposicional

Las fórmulas de la lógica proposicional son aquellas que obtenemos aplicando un número finito de veces las reglas que aparecen a continuación, y sólo ellas:

1. Todas las variables proposicionales $p,q,r,\mathrm{\dots },p_1,q_1,r_1,\mathrm{\dots }$ son fórmulas de la lógica proposicional.

2. Si ${\phi }_1$ y ${\phi }_2$ son fórmulas de la lógica proposicional, entonces también lo son $(\neg {\phi }_1)$, $(\phi \vee {\phi }_2)$, $({\phi }_1\wedge {\phi }_2)$, $({\phi }_1\to {\phi }_2)$ y $({\phi }_1\leftrightarrow {\phi }_2)$.

Una definición alternativa usando una gramática en la Forma Backus Naur (BNF por sus siglas en inglés) se presenta enseguida.

Definición 3.2

Las fórmulas de la lógica proposicional son aquellas que se obtienen a partir de la siguiente gramática en BNF.

$$\phi ::=p|(\neg \phi )|(\phi \vee \phi )|(\phi \wedge \phi )|(\phi \to \phi )|(\phi \leftrightarrow \phi )$$ (1)

donde $p$ representa cualquier proposición atómica, y cada presencia de $\phi$ a la derecha de $::=$ representa cualquier fórmula ya construida. Adicionalmente, las dos constantes sintácticas booleanas son $\top$ y $⟂$.

Precedencia: $\neg$ tiene mayor precedencia que $\vee$ y $\wedge$, estos dos conectivos tienen mayor precedencia que $\to$, y la implicación tiene mayor precedencia que el bi-condicional $\leftrightarrow$. Los operadores $\vee$, $\wedge$ y $\leftrightarrow$ son asociativos, mientras que la implicación $\to$ se asocia a la derecha, por ejemplo, $p\to q\to r$ denota $p\to (q\to r)$. Así, $p\vee \neg q\to r\leftrightarrow q\wedge \neg p$ es equivalente a $((p\vee (\neg q))\to r)\leftrightarrow (q\wedge (\neg p))$.

¿Cómo mostramos que una cadena es una fórmula? ¿Es $\phi$ una fórmula, donde $\phi$ es

$(((\neg p)\wedge q)\to (p\wedge (q\vee (\neg r))))$ ?

la respuesta se facilita al notar que la gramática (1) satisface el principio de inversión, lo que significa que podemos invertir el proceso de construcción de fórmulas, es decir, en la gramática siempre hay una única cláusula que fue aplicada al último. Para la fórmula de arriba, la última regla aplicada fue la quinta cláusula, por lo que $\phi$ es una implicación con antecedente $((\neg p)\wedge q)$ y consecuente $(p\wedge (q\vee (\neg r)))$. Al emplear el principio de inversión al antecedente, vemos que es la conjunción de $(\neg p)$ y $q$. Luego, $(\neg p)$ resulta de aplicar la segunda cláusula sobre la fórmula $p$, que resulta de aplicar la primer cláusula. Por esta misma cláusula $q$ es una fórmula. De manera similar podemos aplicar el principio de inversión para concluir que el consecuente $(p\wedge (q\vee (\neg r))))$ es una fórmula.

La Figura 1 muestra el árbol de análisis sintáctico de la fórmula $\phi$. En esta representación los paréntesis son innecesarios ya que las trayectorias y la estructura ramificada elimina cualquier ambigüedad al interpretar a $\phi$. Mientras que en la representación lineal de $\phi$, la estructura ramificada del árbol se conserva al insertar paréntesis como se hace en la definición de fórmulas.

Figura 1: Un árbol de análisis sintáctico para la fórmula $(((\neg p)\wedge q)\to (p\wedge (q\vee (\neg r))))$.

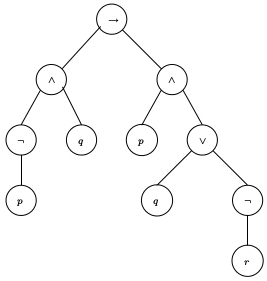
La manera más sencilla de verificar que una cadena de símbolos $\phi$ es una fórmula es intentar construir su árbol de derivación.

Al considerar los árboles de análisis sintáctico podemos entender nociones como el concepto de subfórmula. Dada la fórmula $\phi$ definida arriba, sus subfórmulas son aquellas que corresponden a los subárboles del árbol en la Figura 1.

4 Inducción estructural

Teorema 4.1 (Inducción estructural)

Para demostrar que una propiedad es cierta para toda fórmula $\phi$ de la lógica proposicional:

1. Demuestre que la propiedad es cierta para todo átomo $p$.

2. Suponga que la propiedad es cierta para una fórmula $\phi$ y demuestre que la propiedad se cumple para $\neg \phi$.

3. Suponga que la propiedad es cierta para las fórmulas $\phi$ y $\psi$, y demuestre que la propiedad se cumple para $\phi \bowtie \psi$, donde $\bowtie$ corresponde a cada conectivo lógico binario.

5 Semántica

Definición 5.1

Un estado o una asignación de las variables proposicionales es una función $I$ que asigna a cada variable proposicional el valor de falso $(0)$ o verdadero $(1)$,

$$I:\text{Variables proposicionales}\to \{\mathrm{0,1}\}.$$

Dadas $n$ variables proposicionales existen $2^n$ estados distintos para tales variables.

Definición 5.2

Dado un estado de las variables $I$, definimos la interpretación de las fórmulas con respecto a $I$ como la función $I^{\star }$, que asigna valores de verdad a las fórmulas de la lógica proposicional:

• $I^{\star }(p)=I(p)$ para toda variable proposicional $p$,

• $I^{\star }(\top )=1$,

• $I^{\star }(\perp )=0$,

• $I^{\star }(\neg \phi )=1$ syss $I^{\star }(\phi )=0$,

• $I^{\star }(\phi \vee \psi )=0$ syss $I^{\star }(\phi )=I^{\star }(\psi )=0$,

• $I^{\star }(\phi \wedge \psi )=1$ syss $I^{\star }(\phi )=I^{\star }(\psi )=1$,

• $I^{\star }(\phi \to \psi )=0$ syss $I^{\star }(\phi )=1$ e $I^{\star }(\psi )=0$, y

• $I^{\star }(\phi \leftrightarrow \psi )=1$ syss $I^{\star }(\phi )=I^{\star }(\psi )$.

Un estado de las variables $I$ genera de manera única a la interpretación $I^{\star }$ por lo que de ahora en adelante escribiremos $I$ en lugar de $I^{\star }$. Esto se conoce como sobrecarga de operadores.

5.1 Declaración condicional en español

Como la declaración condicional o implicación juega un papel muy importante en el razonamiento matemático, una variedad de terminología se usa para expresar $p\to q$. La mayoría de las maneras de expresar la implicación en español se pueden encontrar a continuación:

• si $p$, entonces $q$

• si $p$, $q$

• $p$ es suficiente para $q$

• $q$ si $p$

• $q$ cuando $p$

• una condición necesaria para $p$ es $q$

• $q$ a menos que $\neg p$

• $p$ implica $q$

• $p$ solo si $q$

• una condición suficiente para $q$ es $p$

• $q$ siempre que $p$

• $q$ es necesaria para $p$

• $q$ se sigue de $p$

Para recordar la traducción correcta de “$p$ solo si $q$” y de “una condición necesaria para $p$ es $q$” notemos que de estos enunciamos podemos concluir que si $q$ no se cumple, entonces $p$ tampoco. Es decir, los enunciados son falsos si $p$ es verdadero y $q$ falso; son verdaderos de otro modo. Ambas declaraciones presentan un mismo comportamiento que $p\to q$.

Khan Academy menciona lo siguiente sobre la traducción de la oración “$q$ es condición necesaria para $p$”:

Para alcanzar un objetivo $p$ hay un requisito u obligación $q$. Lo más importante que debes saber sobre las condiciones necesarias es que no garantizan ningún tipo de resultado.

Por ejemplo, “pagar la tarifa de la visa americana es necesario para obtenerla”, pero realizar el pago no garantiza que se obtenga ya que también se toma en consideración la información en la solicitud, estados financieros, y la entrevista en la embajada/consulado, entre otros. Así, $q$ se tiene que cumplir para que ocurra $p$, pero no hay garantía de que al cumplir con la condición necesaria $q$ se lleve a cabo $p$. Lo que sí es seguro es que si se alcanza el objetivo, entonces se cumplió con el requisito, i.e., $p\to q$.

La frase “a menos” es usada para expresar una declaración condicional. Observemos que “$q$ a menos que $\neg p$” significa que si $\neg p$ es falsa, entonces $q$ debe ser cierta. Es decir, la declaración “$q$ a menos que $\neg p$” es falsa cuando $p$ es verdadera y $q$ es falsa, de otro modo es verdadera. Por consiguiente, “$q$ a menos que $\neg p$” y $p\to q$ tienen siempre el mismo valor de verdad.

5.2 Valor de verdad de la implicación

Una manera útil de entender el valor de verdad de la implicación es considerarla como un contrato u obligación. Por ejemplo, la promesa que muchos políticos hacen cuando hay elecciones es:

“Si me eligen, entonces reduciré los impuestos.”

Si el político es electo, los electores esperarían que el político redujera los impuestos. Si el político no es electo, no se tendría expectativa alguna de que tal persona redujera los impuestos, aunque la persona pudiera tener suficiente influencia sobre los que estén en el poder para reducirlos. Es únicamente cuando el político es electo y no reduce los impuestos que los electores pueden decir que el político ha roto su promesa de campaña. Este último escenario corresponde al caso cuando $p$ es verdadero y $q$ falso en $p\to q$.

5.3 Ejemplo

Dado el significado de las siguientes variables proposicionales,

$$\begin{array}{c}p:\text{el Sr. López está feliz}\hfill \\ q:\text{la Sra. López está feliz}\hfill \\ r:x\text{ es impar}\hfill \\ s:x\text{ es primo}\hfill \\ t:\text{la secuencia }{\alpha }_n\text{ converge}\hfill \\ u:\text{la secuencia }{\alpha }_n\text{ está acotada}\hfill \\ v:\text{Kasparov ganará el torneo de ajedrez}\hfill \\ w:\text{Kasparov gana hoy}\hfill \end{array}$$

indique una fórmula de la lógica proposicional que corresponda a cada una de las expresiones siguientes:

1. Si el Sr. López está feliz, la Sra. López no está feliz, y si el Sr. López no está feliz, la Sra. López no está feliz.

2. El Sr. López está feliz y la Sra. López no, o el Sr. López no está feliz y la Sra. López sí.

3. Una condición suficiente para que $x$ sea impar es que $x$ es primo.

4. Una condición necesaria para que $x$ sea impar es que $x$ sea primo.

5. La secuencia ${\alpha }_n$ converge si está acotada.

6. La secuencia ${\alpha }_n$ converge solo si está acotada.

7. Kasparov ganará el torneo de ajedrez a menos que Kasparov gane hoy.

8. Kasparov ganará el torneo de ajedrez si y solo si Kasparov gana hoy.

6 Sustitución

La operación de sustitución de las presencias de la variable proposicional $p$ por la fórmula $\psi$ en la fórmula $\phi$, denotada por $\phi [p:=\psi ]$, se define recursivamente como:

donde $\bowtie =\{\wedge ,\vee ,\to ,\leftrightarrow \}$

Similarmente se puede definir la sustitución simultánea $\phi [p_1,\mathrm{\dots },p_n:={\psi }_1,\mathrm{\dots },{\psi }_n]$, denotada como $\phi [\overrightarrow{p}:=\overrightarrow{\psi }]$.

La sustitución tiene las siguientes propiedades:

• $\phi [p:=\psi ]=\phi$ si $p$ no está presente en $\phi$.

• $\phi [p:=\psi ][q:=\chi ]=\phi [q:=\chi ][p:=\psi [q:=\chi ]]$ si $p\ne q$ y $p$ no está presente en $\chi$.

• $\phi [\overrightarrow{q},p:=\overrightarrow{\psi },\chi ]=\phi [\overrightarrow{q}:=\overrightarrow{\psi }][p:=\chi ]$ si $p\notin \{\overrightarrow{q}\}$ y $p$ no está presente en $\overrightarrow{\psi }$.

Ejemplo 6.1

Realice la sustitución que viene a continuación y elimine los paréntesis redundantes:

7 Conceptos semánticos básicos

Sea $\phi$ una fórmula. Entonces,

• $\phi$ es una tautología, o fórmula válida, si $I(\phi )=1$ para toda interpretación $I$. En tal caso escribimos $\vDash \phi$.

• La interpretación $I$ es un modelo de $\phi$ si $I(\phi )=1$. En tal caso escribimos $I\vDash \phi$, y catalogamos a $\phi$ como satisfacible.

• La interpretación $I$ no es un modelo de $\phi$ si $I(\phi )=0$. En tal caso escribimos $I\vDash ̸\phi$.

• $\phi$ es una contradicción, o fórmula insatisfacible, si $I(\phi )=0$ para toda interpretación $I$.

• $\phi$ es contingente si existen interpretaciones $I$ e $I^{\prime }$, tales que $I(\phi )=1$ e $I^{\prime }(\phi )=0$.

Sea $\mathrm{\Gamma }$ un conjunto de fórmulas.

• $\mathrm{\Gamma }$ es satisfacible si existe una interpretación $I$ tal que $I(\phi )=1$ para toda $\phi \in \mathrm{\Gamma }$.

• $\mathrm{\Gamma }$ es insatisfacible si no existe una interpretación $I$ tal que $I(\phi )=1$ para toda $\phi \in \mathrm{\Gamma }$.

Se extiende de la manera usual la función de interpretación de fórmulas para que también se aplique a conjuntos de fórmulas. De manera que podamos escribir $I(\mathrm{\Gamma })=1$ si $\mathrm{\Gamma }$ es satisfacible por $I$.

Proposición 7.1

Sea $\mathrm{\Gamma }=\{{\phi }_1,\mathrm{\dots },{\phi }_n\}$ un conjunto de fórmulas.

• $\mathrm{\Gamma }$ es satisfacible si y solo si ${\phi }_1\wedge \mathrm{\dots }\wedge {\phi }_n$ es satisfacible.

• $\mathrm{\Gamma }$ es insatisfacible si y solo si ${\phi }_1\wedge \mathrm{\dots }\wedge {\phi }_n$ es una contradicción.

Lema 7.2

El conjunto vacío de fórmulas, $\mathrm{\varnothing }$, es válido.

Demostración. Un conjunto de fórmulas es válido syss toda fórmula en el conjunto es verdadera bajo cualquier interpretación. De otro modo, hay un fórmula $\phi \in \mathrm{\varnothing }$ que alguna interpretación no satisface. Pero decir que hay una fórmula en $\mathrm{\varnothing }$ está mal. Por lo tanto, $\mathrm{\varnothing }$ es un conjunto de fórmulas válido. $\mathbf{⊣}$

Equivalencia de Fórmulas

Sean $\phi$ y $\psi$ dos fórmulas. Decimos que son equivalentes si $I(\phi )=I(\psi )$ para toda interpretación $I$. Lo denotamos como $\phi \equiv \psi$.

Proposición 7.3

Sean $\phi$ y $\psi$ dos fórmulas. Se cumple que $\phi \equiv \psi$ si y solo si $\vDash \phi \leftrightarrow \psi$.

Proposición 7.4 (Regla de Leibniz)

Si $\phi \equiv \psi$ y $p$ es una variable proposicional, entonces $\tau [p:=\phi ]\equiv \tau [p:=\psi ]$.

Consecuencia lógica

Sean $\mathrm{\Gamma }$ un conjunto de fórmulas y $\phi$ una fórmula. Decimos que $\phi$ es consecuencia lógica de $\mathrm{\Gamma }$, lo cual se denota como $\mathrm{\Gamma }\vDash \phi$, si para toda interpretación $I$ que satisface a $\mathrm{\Gamma }$, entonces $I$ también satisface a $\phi$.

La relación de consecuencia lógica se entiende a través de una implicación del siguiente modo:

$$\text{para toda interpretación }I\text{,}I(\mathrm{\Gamma })=1\to I(\phi )=1$$

lo que nos indica que siempre que $I$ satisfaga a $\mathrm{\Gamma }$, entonces necesariamente $I$ satisface a $\phi$. Para corroborar una consecuencia lógica se debe tomar una interpretación $I$ cualquiera que suponemos satisface a $\mathrm{\Gamma }$, y debe probarse que esa misma $I$ también satisface a $\phi$.

Proposición 7.5

La consecuencia lógica cumple las siguientes propiedades:

• Si $\phi \in \mathrm{\Gamma }$, entonces $\mathrm{\Gamma }\vDash \phi$.

• $\phi$ es tautología syss $\mathrm{\varnothing }\vDash \phi$.

• $\mathrm{\Gamma }\vDash \phi \to \psi$ syss $\mathrm{\Gamma }\cup \{\phi \}\vDash \psi$.

• Si $\mathrm{\Gamma }$ es insatisfacible, entonces $\mathrm{\Gamma }\vDash \phi$ para toda fórmula $\phi$.

• Principio de refutación: $\mathrm{\Gamma }\vDash \phi$ syss $\mathrm{\Gamma }\cup \{\neg \phi \}$ es insatisfacible.

Demostración. Se demostrará el Principio de refutación, los demás incisos se dejan como ejercicio. Dicho principio es equivalente a demostrar que $\mathrm{\Gamma }\vDash ̸\phi$ syss $\mathrm{\Gamma }\cup \{\neg \phi \}$ es satisfacible. Así,

$\mathbf{⊣}$

Correctud de argumentos lógicos

Un argumento lógico es una sucesión de fórmulas ${\phi }_1,\mathrm{\dots },{\phi }_n$ que llamamos premisas y una fórmula $\psi$ que llamamos conclusión.

Un argumento con premisas ${\phi }_1,\mathrm{\dots },{\phi }_n$ y conclusión $\psi$ es lógicamente correcto si la conclusión se sigue lógicamente de las premisas, i.e., $\{{\phi }_1,\mathrm{\dots },{\phi }_n\}\vDash \psi$.

Ejemplo 7.6

Supongamos que estamos en la isla de los caballeros y de los bribones. En esta isla todos son o caballeros o bribones. Los caballeros siempre dicen la verdad y los bribones siempre mienten. En una ocasión, hubo una epidemia que causaba que los caballeros enfermos siempre dijesen mentiras y que los bribones enfermos siempre dijesen la verdad. ¿Cuál de las siguientes oraciones puede ser dicha por un caballero enfermo?

1. Soy un caballero.

2. Si soy un caballero, entonces estoy enfermo.

3. Soy un bribón enfermo.

4. O bien soy un caballero enfermo, o bien soy un bribón enfermo.

5. Si estoy sano, entonces soy un caballero.

Ejemplo 7.7

Sean $\mathrm{\Gamma }$ y $\mathrm{\Delta }$ dos conjuntos de oraciones de la lógica proposicional, y sean $\phi$ y $\psi$ fórmulas de la lógica proposicional. Determine para cada una de las siguientes afirmaciones si es verdadera, con una demostración, o si es falsa, con un contraejemplo.

• Si $\mathrm{\Gamma }\vDash \phi$ y $\mathrm{\Delta }\vDash \phi$, entonces $\mathrm{\Gamma }\cap \mathrm{\Delta }\vDash \phi$.

• Si $\mathrm{\Gamma }\vDash \phi$ y $\mathrm{\Delta }\vDash \phi$, entonces $\mathrm{\Gamma }\cup \mathrm{\Delta }\vDash \phi$.

• Si $\mathrm{\Gamma }\vDash \phi$ y $\mathrm{\Delta }\vDash ̸\phi$, entonces $\mathrm{\Gamma }\cup \mathrm{\Delta }\vDash \phi$.

• Si $\mathrm{\Gamma }\vDash ̸\psi$, entonces $\mathrm{\Gamma }\vDash \neg \psi$.

• Si $\mathrm{\Gamma }\vDash \neg \psi$, entonces $\mathrm{\Gamma }\vDash ̸\psi$.