Lógica Computacional
Nota 03. Reglas de deducción natural y propiedades de los sistemas de demostración.¹¹El material aquí presentado se basa el libro de Huth y Ryan, Logic in Computer Science.

Noé Salomón Hernández S

Los sistemas de demostración son herramientas para verificar la validez de argumentos lógicos por medios sintácticos.

¿Cómo es que podemos construir un sistema de demostración para razonar acerca de proposiciones, de modo que podamos establecer la validez de argumentos lógicos? Un sistema de demostración está formado por un conjunto de reglas de inferencia. De modo que una demostración es un conjunto de fórmulas que permiten ir de las premisas a la conclusión por medio de transformaciones sintácticas.

En deducción natural, tenemos una colección de dichas reglas de inferencia. Estas reglas nos permiten inferir fórmulas de otras fórmulas. Al aplicar estas reglas en sucesión, podemos inferir una conclusión a partir de un conjunto de premisas.

Supongamos que tenemos un conjunto de premisas $\varphi_{1},\ldots,\varphi_{n}$ y una conclusión $\psi$ . Al aplicar las reglas de inferencia a las premisas, esperamos conseguir nuevas fórmulas, para seguir aplicando reglas de inferencia sobre las premisas y las fórmulas recién inferidas, buscamos llegar a la conclusión en algún momento. Esta situación la denotamos como

\varphi_{1},\ldots,\varphi_{n}\vdash\psi\mathchar 46\relax

Esta expresión se llama secuente; es válido si de las premisas llegamos a la conclusión por medio de reglas de inferencia.

1 Deducción natural

La deducción natural tiene reglas para introducir o eliminar los conectivos lógicos. Algunas reglas contemplan la introducción de hipótesis adicionales. Por esta razón, las inferencias que se hagan utilizando estas hipótesis aparecen dentro de cajas. Las cajas se pueden cerrar extrayendo una conclusión de acuerdo con las condiciones de cada regla. Las reglas de deducción natural se resumen en la Figura 1.

\begin{array}[]{c|cc}&\text{\sf Introducción}&\text{\sf Eliminación}\\ \hline\cr\\[0.50003pt] \wedge&\dfrac{\varphi\quad\psi}{\varphi\wedge\psi}(I{\scriptstyle\wedge})&% \dfrac{\varphi\wedge\psi}{\varphi}(E{\scriptstyle\wedge}_{1})\qquad\dfrac{% \varphi\wedge\psi}{\psi}(E{\scriptstyle\wedge}_{2})\\[22.0pt] \vee&\dfrac{\varphi}{\varphi\vee\psi}(I{\scriptstyle\vee}_{1})\qquad\dfrac{% \psi}{\varphi\vee\psi}(I{\scriptstyle\vee}_{2})&\dfrac{\varphi\vee\psi\quad% \boxed{\begin{array}[]{c}\varphi\\ \vdots\\ \chi\end{array}}\quad\boxed{\begin{array}[]{c}\psi\\ \vdots\\ \chi\end{array}}}{\chi}(E{\scriptstyle\vee})\\[22.0pt] \rightarrow&\dfrac{\boxed{\begin{array}[]{c}\varphi\\ \vdots\\ \psi\end{array}}}{\varphi\rightarrow\psi}(I{\scriptstyle\rightarrow})&\dfrac{% \varphi\quad\varphi\rightarrow\psi}{\psi}(E{\scriptstyle\rightarrow})\\[35.000% 05pt] \leftrightarrow&\dfrac{\varphi\rightarrow\psi\quad\psi\rightarrow\varphi}{% \varphi\leftrightarrow\psi}(I{\scriptstyle\leftrightarrow})&\dfrac{\varphi% \leftrightarrow\psi}{\varphi\rightarrow\psi}(E{\scriptstyle\leftrightarrow}_{1% })\qquad\dfrac{\varphi\leftrightarrow\psi}{\psi\rightarrow\varphi}(E{% \scriptstyle\leftrightarrow}_{2})\\[30.00005pt] \neg&\dfrac{\boxed{\begin{array}[]{c}\varphi\\ \vdots\\ \perp\end{array}}}{\neg\varphi}(I{\scriptstyle\neg})&\dfrac{\varphi\quad\neg% \varphi}{\perp}(E{\scriptstyle\neg})\\[25.00003pt] \perp&\text{no hay regla de introducción para }\perp&\dfrac{\perp}{\varphi}(E{% \scriptstyle\perp})\\[25.00003pt] \neg\neg&&\dfrac{\neg\neg\varphi}{\varphi}(E{\scriptstyle\neg\neg})\end{array}

Algunas reglas derivadas de utilidad

\begin{array}[]{>{\centering\arraybackslash$} p{10em} <{$} >{\centering% \arraybackslash$} p{10em} <{$} }\dfrac{\varphi\rightarrow\psi\quad\neg\psi}{% \neg\varphi}(MT)$\@add@centering&\dfrac{\varphi}{\neg\neg\varphi}(I{% \scriptstyle\neg\neg})$\@add@centering\cr[1{,}7em]\dfrac{\boxed{\begin{array}[% ]{c}\neg\varphi\\ \vdots\\ \perp\end{array}}}{\varphi}(PPC)$\@add@centering&\dfrac{}{\varphi\vee\neg% \varphi}(LTE)$\@add@centering\end{array}

Figura 1: Reglas de deducción natural para la lógica proposicional.

A continuación damos la intuición de las reglas de deducción natural:

$I{\scriptstyle\wedge}$ dice que para demostrar $\varphi\wedge\psi$ , debemos demostrar primero $\varphi$ y $\psi$ de manera separada, y entonces usar la regla $I{\scriptstyle\wedge}$ .
$E{\scriptstyle\wedge}_{1}$ dice que para demostrar $\varphi$ , hay intentar demostrar $\varphi\wedge\psi$ y entonces usar la regla $E{\scriptstyle\wedge}_{1}$ . Esto no parece muy brillante porque probablemente demostrar $\varphi\wedge\psi$ es más complicado que demostrar $\varphi$ por sí sola. Sin embargo, puede ser que ya se tenga $\varphi\wedge\psi$ en algún lado de la derivación, es en ese caso cuando la regla es útil.
$I{\scriptstyle\vee}_{1}$ dice que para demostrar $\varphi\vee\psi$ , hay que demostrar $\varphi$ . En general es más difícil demostrar $\varphi$ que demostrar $\varphi\vee\psi$ , así que esta regla es típicamente útil si de algún modo logramos demostrar $\varphi$ .
$E{\scriptstyle\vee}$ dice que si se tiene $\varphi\vee\psi$ , y se desea demostrar una fórmula $\chi$ , entonces debemos intentar demostrar $\chi$ a partir de $\varphi$ , y a su vez demostrar $\chi$ a partir de $\psi$ . (En tales demostraciones, podemos usar las otras premisas disponibles también).
$I{\scriptstyle\rightarrow}$ dice que si deseamos demostrar $\varphi\rightarrow\psi$ , debemos demostrar $\psi$ a partir de $\varphi$ (y de las otras premisas disponibles).
$I{\scriptstyle\neg}$ dice que para demostrar $\neg\varphi$ , tenemos que demostrar $\bot$ a partir de $\varphi$ (y de las otras premisas disponibles).

Tome en cuenta las siguientes observaciones:

✓

En la regla $E{\scriptstyle\wedge}_{1}$ , la conclusión $\varphi$ tiene que ser la misma que el primer elemento de la conjunción, mientras que la naturaleza de la segunda fórmula $\psi$ es irrelevante.
✓

Las cajas en las demostraciones sirven para delimitar el alcance de las hipótesis temporales en cuestión. Al abrir una caja se inicia con la hipótesis temporal, digamos $p$ . Continuamos aplicando reglas para obtener fórmulas con normalidad, solo que tales fórmulas dependen de la hipótesis. Finalmente, obtenemos una fórmula, digamos $q$ , con la que cerramos la caja e inmediatamente después debemos escribir la conclusión. En el supuesto en el que aplicamos $I{\scriptstyle\rightarrow}$ , se debe concluir con $p\rightarrow q$ . Dicha conclusión no depende de la hipótesis temporal.
✓

Podemos usar una fórmula $\varphi$ en cualquier momento de una demostración solamente si dicha fórmula aparece antes, y esa presencia de $\varphi$ no está dentro de una caja ya cerrada.
✓

La fórmula que inmediatamente sigue a una caja cerrada debe ser la conclusión de la regla que usa tal caja.
✓

Algunas partes de la demostración pueden ser determinadas por la estructura de la fórmula a demostrar, mientras que otras partes de la demostración requieren creatividad e ingenio. Considere la demostración del secuente $\vdash(q\rightarrow r)\rightarrow((\neg q\rightarrow\neg p)\rightarrow(p% \rightarrow r))$ .
✓
Acerca de la regla $E{\scriptstyle\vee}$ podemos mencionar que:
- •
  
  La conclusión en cada uno de los casos es la misma fórmula (la $\chi$ en la regla $E{\scriptstyle\vee}$ ).
- •
  
  Durante el análisis de cada caso quizá no se pueda usar la otra hipótesis temporal, a menos que sea una fórmula que haya sido demostrada antes de abrir las cajas correspondientes a la regla $E{\scriptstyle\vee}$ .
✓

La regla copia permite repetir una fórmula que aparece con anterioridad, a menos que tal fórmula dependa de hipótesis temporales cuyas cajas ya están cerradas. Considere el secuente $\vdash p\rightarrow(q\rightarrow p)$ cuya validez puede ser demostrada como sigue:

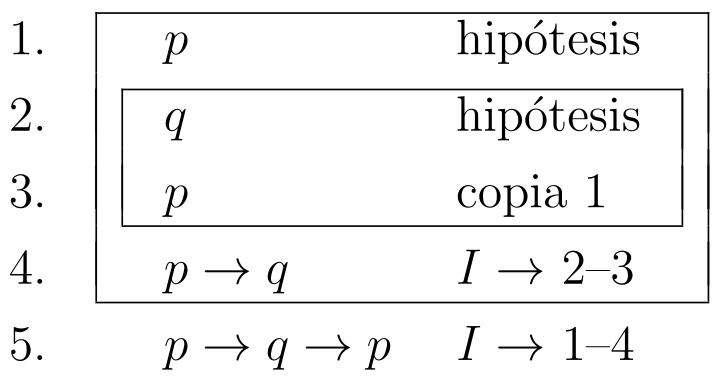
Definición 1.1

Una fórmula $\varphi$ con secuente válido $\vdash\!\varphi$ se conoce como teorema.

Ejercicios

Demuestre los siguientes teoremas por deducción natural:

i)

$\vdash((p\wedge q)\rightarrow r)\rightarrow p\rightarrow q\rightarrow r$
ii)

$\vdash(p\rightarrow q)\rightarrow(p\wedge r\rightarrow q\wedge r)$
iii)

$\vdash(p\rightarrow q)\rightarrow(p\vee r\rightarrow q\vee r)$
iv)

$\vdash p\rightarrow q\rightarrow(p\wedge q)$
v)

$\vdash(p\wedge q\rightarrow r)\rightarrow(p\rightarrow q\rightarrow r)$
vi)

$\vdash\varphi\vee\neg\varphi$

Demuestre los siguientes secuentes por deducción natural.

i)

$p\rightarrow(q\rightarrow r),\ p,\neg r\vdash\neg q$
ii)

$p\wedge\neg q\rightarrow r,\neg r,\ p\vdash q$
iii)

$\varphi\rightarrow\psi,\neg\psi\vdash\neg\varphi$ , este secuente se conoce como Modus Tollens.
iv)

$p\rightarrow q\vdash\neg p\vee q$

2 Propiedades de los sistemas de demostración

Sea $\vdash$ el sistema de demostración por deducción natural aquí propuesto, y sean $\varphi_{1},\ldots,\varphi_{n}$ y $\psi$ fórmulas. Para el sistema $\vdash$ se tiene que es:

i

Correcto. Si $\varphi_{1},\ldots,\varphi_{n}\vdash\psi$ implica que $\varphi_{1},\ldots,\varphi_{n}\models\psi$ .
ii

Completo. Si $\varphi_{1},\ldots,\varphi_{n}\models\psi$ implica que $\varphi_{1},\ldots,\varphi_{n}\vdash\psi$ .
iii

Consistente. No existe una fórmula $\chi$ tal que $\vdash\chi$ y $\vdash\neg\chi$ .

Al combinar las dos primeras propiedades obtenemos:

\varphi_{1},\ldots,\varphi_{n}\vdash\psi\text{\ si y solo si\ }\varphi_{1},% \ldots,\varphi_{n}\models\psi

Así que bien podríamos optar por trabajar con cualquiera de las dos maneras: semántica o sintácticamente. El método sintáctico tiene que ver con la búsqueda de una demostración, que es la base de la programación lógica. El método semántico nos obliga a calcular la tabla de verdad, la cual tiene un tamaño exponencial en el número de proposiciones atómicas en la fórmula. Ambos métodos no son viables en general, aunque instancias particulares de las fórmulas a menudo responden de forma diferente al emplear estos dos métodos.

Ejercicios 2.1

Determine si el siguiente argumento lógico es correcto mediante deducción natural: