Lógica Computacional
Nota 04. Tableaux semánticos

1 Tableaux semánticos

El método de tableaux semánticos es un procedimiento de decisión que determina si una fórmula de la lógica proposicional es satisfacible, se basa en la búsqueda de un modelo mediante la descomposición de la fórmula en conjuntos de proposiciones atómicas, que pueden estar negadas. Tales conjuntos son satisfacibles si no cuentan con una proposición atómica $p$ y su negación $\neg p$. La fórmula en cuestión es satisfacible si uno de estos conjuntos lo es.

Definición 1.1

Una literal es una proposición atómica o su negación. Una proposición atómica es una literal positiva y la negación de una proposición atómica es una literal negativa. Para cualquier proposición atómica $p$, un par de literales complementarias es $\{p,\neg p\}$.

Podemos extender esta idea a un conjunto de fórmulas, de manera que determinar si es satisfacible se reduce a analizar su conjunto de literales.

Teorema 1.2

Un conjunto de literales es satisfacible si y solo si no contiene un par de literales complementarias.

2 Construcción de tableaux semánticos

En este método las fórmulas etiquetan nodos de un árbol, donde cada trayectoria indica las fórmulas que deben satisfacerse en una posible interpretación.

Las fórmulas iniciales etiquetan la raíz del árbol. Cada nodo se expande en uno o dos nodos hijos dependiendo de la descomposición de la fórmula en cuestión. Las hojas se etiquetan con literales. Una hoja etiquetada con literales complementarias se marca con ✗, de otro modo se marca con ✓.

2.1 Algoritmo

Input: Un conjunto de fórmulas $\{{\gamma }_1,\mathrm{\dots },{\gamma }_n\}$ de la lógica proposicional. Considere activas a las fórmulas ${\gamma }_i$ que no son literales.

Output: Un tableaux semántico $𝒯$ para $\{{\gamma }_1,\mathrm{\dots },{\gamma }_n\}$ cuyas ramas están marcadas

Inicialmente, $𝒯$ consiste de un nodo raíz etiquetado con $\{{\gamma }_1,\mathrm{\dots },{\gamma }_n\}$. Si únicamente hay literales en este nodo raíz, dirigirse al paso 3 que se describe abajo.

Repetir lo siguiente mientras que en una rama no marcada $b$ haya una fórmula $\phi$ activa:

1. Clasifique a $\phi$ como una fórmula $\alpha$ o $\beta$ según lo estipulado en la Figura 1. Descompóngala como corresponda de acuerdo a las acciones que aparecen enseguida,

   • Si $\phi$ es una fórmula $\alpha$, agregue una hoja ${\mathrm{\ell }}^{\prime }$ como extensión de la rama $b$. Etiquete a ${\mathrm{\ell }}^{\prime }$ como $\{{\phi }_1,{\phi }_2\}$.

   • Si $\phi$ es una fórmula $\beta$, agregue dos nuevas hojas ${\mathrm{\ell }}^{\prime }$ y ${\mathrm{\ell }}^{\prime \prime }$ como extensiones independientes de la rama $b$. Etiquete a ${\mathrm{\ell }}^{\prime }$ como $\{{\phi }_1\}$, y etiquete a ${\mathrm{\ell }}^{\prime \prime }$ como $\{{\phi }_2\}$.

2. Desactive a $\phi$ si se ha descompuesto en todas las ramas no marcadas en las que figura en un recorrido hacia la raíz.

3. Si resulta una rama a lo largo de la cual hay un par de literales complementarias, marque dicha rama como cerrada ✗. Marque como abiertas ✓ aquellas ramas que no tienen literales complementarias ni fórmulas activas.

Figura 1: Clasificación de fórmulas $\alpha$ y $\beta$. Las fórmulas se clasifican con base a su conectivo principal. Si es una negación, la clasificación considera tanto a la negación como al conectivo principal de la fórmula negada. Las fórmulas $\alpha$ son conjuntivas y las $\beta$ disyuntivas.

Definición 2.1

Un tableaux está cerrado si todas sus hojas están marcadas con ✗, de otro modo está abierto.

El algoritmo para construir tableaux no es determinista ya que en la mayoría de los pasos se tiene una elección en la hoja a expandir y en la fórmula a descomponer. De modo que se recomienda lo siguiente:

• Descomponer una fórmula $\alpha$ primero que una $\beta$.

• Una rama se puede cerrar cuando un nodo tiene a una fórmula y a su negación, y no solo cuando figure un par de literales complementarias. Por ejemplo, no hay razón para seguir expandiendo un nodo que tenga a: $(p\wedge (q\vee r)),\neg (p\wedge (q\vee r))$.

Ejemplo 2.2

Determine si el conjunto de fórmulas siguiente es satisfacible mediante tableaux: $\{p,\neg q\vee r,\neg s\to s,\neg s\}$

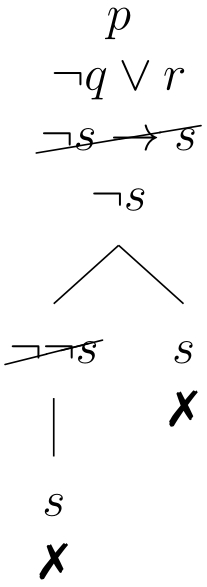
Observe que la fórmula $\neg q\vee r$ está activa, pero como todas las ramas están marcadas la construcción del tableaux ha terminado. El conjunto es insatisfacible ya que el tableaux está cerrado.

3 El método de tableaux semántico es correcto y completo

Vamos a conectar la salida del tableaux (que esté cerrado o no) con el concepto semántico de verdad.

Teorema 3.1

El algoritmo descrito arriba es correcto y completo. Sea $𝒯$ un tableaux para una fórmula $\phi$. $𝒯$ está cerrado si y solo si $\phi$ es insatisfacible.

Corolario 3.2

$\phi$ es satisfacible si y solo si $𝒯$ está abierto.

Corolario 3.3

$\phi$ es una tautología si y solo si el tableaux para $\neg \phi$ se cierra.

4 Tableaux semánticos para determinar si un argumento lógico es correcto

Dado el principio de refutación, podemos determinar si un argumento lógico $\mathrm{\Gamma }\vDash \psi$ es correcto o no al considerar el conjunto de fórmulas $\mathrm{\Gamma }\cup \{\neg \psi \}$, y construir su tableaux semántico. Si todas las ramas se cierran, el argumento es correcto. Si queda al menos una rama abierta, el argumento es incorrecto.

Ejercicios 4.1

Determinar si los siguientes argumentos son correctos mediante tableaux semánticos:

• Si tengo pies, entonces no tengo guantes. Si tengo calcetines, entonces no tengo manos. Tengo calcetines o tengo guantes. Por lo tanto, si tengo manos, entonces no tengo pies.

  ¿Qué sucede si la conclusión es: No tengo manos y no tengo pies?

• Si Sarah Connor destruye a Skynet en 1994, entonces no habrá Día del Juicio Final. Si no hay Día del Juicio Final, John Connor no enviará a su padre a 1984. Es condición necesaria que John Connor envíe a su padre a 1984, para que el mismo John nazca. Sarah Connor no destruye a Skynet en 1994, si John no nace. Por lo tanto, Sarah Connor no destruirá a Skynet en 1994.

• Si Paula y María son afortunadas, Laura no lo es. Paula es afortunada, y Carlos o Laura lo son. Carlos es afortunado cuando y sólo cuando Ernesto lo es. Por lo tanto, si María es afortunada, Ernesto lo es.