Lógica Computacional
Nota 12. Resolución SLD y programación lógica¹¹Esta nota se base en material elaborado por el prof. Favio Miranda y en el libro de Ben-Ari M., Mathematical Logic for Computer Science

Noé Salomón Hernández S

La resolución fue originalmente desarrollada como un método para la demostración automática de teoremas. Una forma restringida de resolución se usa para obtener cómputos. Un programa se expresa como un conjunto de cláusulas y una consulta o meta es una cláusula que colisiona con las cláusulas de programa. La meta se asume como la negación del resultado del programa. Si la refutación es exitosa, la meta no es consecuencia lógica del programa, pero su negación sí lo es. Las unificaciones que toman lugar durante la refutación constituyen la respuesta buscada.

1 Refutación de una cláusula meta

La teoría de lenguajes formales nos provee de un símbolo de función binario para la concatenación, denotado por el operador infijo $\cdot$ , y tres predicados:

$substr(x,y)$ , $x$ es una subcadena de $y$ .
$prefix(x,y)$ , $x$ es un prefijo de $y$ .
$suffix(x,y)$ , $x$ es un sufijo de $y$ .

Los axiomas de la teoría son:

\begin{array}[]{ll}1\mathchar 46\relax&substr(x,x)\\ 2\mathchar 46\relax&suffix(x,y\cdot x)\\ 3\mathchar 46\relax&prefix(x,x\cdot y)\\ 4\mathchar 46\relax&substr(x,y)\land suffix(y,z)\rightarrow substr(x,z)\\ 5\mathchar 46\relax&substr(x,y)\land prefix(y,z)\rightarrow substr(x,z)\end{array}

En forma clausular tenemos (las cláusulas de programa):

\begin{array}[]{ll}1\mathchar 46\relax&substr(x,x)\\ 2\mathchar 46\relax&suffix(x,y\cdot x)\\ 3\mathchar 46\relax&prefix(x,x\cdot y)\\ 4\mathchar 46\relax&\neg substr(x,y)\lor\neg suffix(y,z)\lor substr(x,z)\\ 5\mathchar 46\relax&\neg substr(x,y)\lor\neg prefix(y,z)\lor substr(x,z)\end{array}

Podemos demostrar que la fórmula $substr(ab,aabc)$ es consecuencia lógica al refutar su negación $\neg substr(ab,aabc)$ , como sigue:

\begin{array}[]{llrl}6\mathchar 46\relax&\neg substr(ab,aabc)&&\\ 7\mathchar 46\relax&\neg substr(ab,y_{1})\lor\neg suffix(y_{1},aabc)&[x:=ab,z:% =aabc]&\text{Res 4,6}\\ 8\mathchar 46\relax&\neg substr(ab,abc)&[x:=abc,y:=a,y_{1}:=abc]&\text{Res 2,7% }\\ &&\text{Una posible unificación entre muchas}\\ 9\mathchar 46\relax&\neg substr(ab,y_{2})\lor\neg prefix(y_{2},abc)&[x:=ab,z:=% abc]&\text{Res 5,8}\\ 10\mathchar 46\relax&\neg substr(ab,ab)&[x:=ab,y:=c,y_{2}:=ab]&\text{Res 3,9}% \\ 11\mathchar 46\relax&\Box&[x:=ab]&\text{Res 1,10}\\ \end{array}

En lugar de determinar si una cláusula meta cerrada es consecuencia lógica de los axiomas, podemos averiguar si $\exists w\ subtr(a,aabc)$ lo es. Vamos a intentar refutar la negación de la fórmula: $\neg\exists w\ subtr(a,aabc)\equiv\forall w\ \neg subtr(a,aabc)$ . Una literal universalmente cuantificada es una cláusula, así que procedemos a la refutación:

\begin{array}[]{rlrl}6\mathchar 46\relax&\neg substr(w,aabc)&&\\ 7\mathchar 46\relax&\neg substr(w,y_{1})\lor\neg suffix(y_{1},aabc)&[x:=w,z:=% aabc]&\text{Res 4,6}\\ 8\mathchar 46\relax&\neg substr(w,bc)&[x:=bc,y:=aa,y_{1}:=bc]&\text{Res 2,7}\\ 9\mathchar 46\relax&\neg substr(w,y_{2})\lor\neg prefix(y_{2},bc)&[x:=w,z:=bc]% &\text{Res 5,8}\\ 10\mathchar 46\relax&\neg substr(w,b)&[x:=b,y:=c,y_{2}:=b]&\text{Res 3,9}\\ 11\mathchar 46\relax&\Box&[w:=b,x:=b]&\text{Res 1,10}\\ \end{array}

No solo demostramos que $\exists w\ \!substr(w,aabc)$ es consecuencia lógica de los axiomas, también hemos realizado un cómputo para determinar el valor $b$ para $w$ que satisface $substr(w,aabc)$ .

2 Cláusulas de Horn y resolución SLD

2.1 Cláusulas de Horn

Definición 2.1.

Una cláusula de Horn es una cláusula de la forma

A\leftarrow B_{1},\ldots,B_{n}\equiv A\vee\neg B_{1}\vee\ldots\vee\neg B_{n}

con a lo más una literal positiva. La literal $A$ es la cabeza y las literales negadas $B_{i}$ son el cuerpo.

Un hecho es una cláusula de Horn unitaria positiva $A\leftarrow$ .
Una cláusula meta es una cláusula de Horn sin literal positiva $\leftarrow B_{1},\ldots,B_{n}$ .
Una cláusula de programa es una cláusula de Horn con una literal positiva y una o más literales negativas.

En programación lógica se prefiere el uso de $\leftarrow$ , el operador de implicación inverso, sobre el operador de implicación hacia adelante $\rightarrow$ . En lugar de $\leftarrow$ podemos optar también por la notación de Prolog, :-.

Definición 2.2.

Los siguientes conceptos serán de utilidad:

Un conjunto de cláusulas de Horn que no sean cláusulas meta y cuyas cabezas tengan el mismo símbolo de predicado es un procedimiento.
Un conjunto de procedimientos es un programa lógico.
Un procedimiento compuesto por hechos sin variables es una base de datos.

Ejemplo 2.3.

El siguiente programa tiene dos procedimientos $P$ y $Q$ ; $P$ es también una base de datos.

1.

$Q(x,y)\leftarrow P(x,y)$ .
2.

$Q(x,y)\leftarrow P(x,z),Q(z,y)$ .

3.

$P(b,a)$ .
4.

$P(c,a)$ .
5.

$P(d,b)$ .
6.

$P(e,b)$ .
7.

$P(f,h)$ .
8.

$P(h,g)$ .
9.

$P(i,h)$ .
10.

$P(j,b)$ .

2.2 Sustitución de respuesta correcta

Definición 2.4.

Sea $P$ un programa y $G$ una cláusula meta. Una sustitución $\theta$ para las variables en $G$ es una sustitución de respuesta correcta si $P\models\forall(\neg G\theta)$ , donde la cuantificación universal se toma sobre todas las variables libres en $\neg G\theta$ .

Observe que la cláusula meta tiene implícitamente la forma negada, que es adecuada para efectuar la refutación por resolución. Así, $\forall(\neg G\theta)$ equivale a una conjunción de literales positivas que se satisface siempre que el programa lógico $P$ se satisfaga. Es decir, dado un programa $P$ , una cláusula meta $G=\neg G_{1}\vee\ldots\vee\neg G_{n}$ , y una sustitución de respuesta correcta $\theta$ , por definición $P\models\forall(\neg G\theta)$ , así:

P\models\forall(G_{1}\wedge\ldots\wedge G_{n})\theta

Por lo tanto, para cualquier sustitución $\sigma$ que convierta a la conjunción anterior en una fórmula sin variables, $(G_{1}\wedge\ldots\wedge G_{n})\theta\sigma$ es verdadera en todo modelo de $P$ . De allí la terminología pues la sustitución $\theta\sigma$ da una respuesta a la consulta expresada por la cláusula meta.

Ejemplo 2.5.

Sea $P$ el conjunto de todos los axiomas de la aritmética.

Sea $G$ la cláusula meta $\neg(6+y=13)$ y $\theta$ la sustitución $[y:=7]$ :

$\begin{array}[]{rcl}\forall(\neg G\theta)&\equiv&\forall(\neg\neg(6+y=13)[y:=7% ])\\ &\equiv&\forall(6+7=13)\\ &\equiv&(6+7=13)\mathchar 46\relax\end{array}$

Como $P\models(6+7=13)$ , $\theta$ es una sustitución de respuesta correcta para $G$ .
Sea $G$ la cláusula meta $\neg(x=y+13)$ y $\theta$ la sustitución $[y:=x-13]$ :

$\begin{array}[]{rcl}\forall(\neg G\theta)&\equiv&\forall(\neg\neg(x=y+13)[y:=x% -13])\\ &\equiv&\forall x(x=x-13+13)\mathchar 46\relax\end{array}$

Como $P\models\forall x(x=x-13+13)$ , $\theta$ es una sustitución de respuesta correcta para $G$ .
Sea $G$ la cláusula meta $\neg(x=y+13)$ y $\theta=\varepsilon$ , la sustitución vacía:

$\begin{array}[]{rcl}\forall(\neg G\theta)&\equiv&\forall(\neg\neg(x=y+13)% \varepsilon)\\ &\equiv&\forall x\forall y(x=y+13)\mathchar 46\relax\end{array}$

Como $P\cancel{\models}\forall x\forall y(x=y+13)$ , $\theta$ no es una sustitución de respuesta correcta para $G$ .

2.3 Resolución SLD

Definición 2.6.

(Resolución SLD) Sea $P$ un programa lógico y $G$ una cláusula meta. Una derivación por resolución SLD es una secuencia de pasos de resolución entre las cláusulas meta y las cláusulas de programa. La primer cláusula meta $G_{0}$ es $G$ . $G_{i+1}$ se deriva de $G_{i}$ seleccionando una literal $A_{i}^{j}\in G_{i}$ , eligiendo un cláusula $C_{i}\in P$ tal que la cabeza de $C_{i}$ unifica con $A_{i}^{j}$ mediante un umg $\theta_{i}$ y realizando:

\begin{array}[]{rcl}G_{i}&=&\leftarrow A_{i}^{1},\ldots,A_{i}^{j-1},A_{i}^{j},% A_{i}^{j+1},\ldots,A_{i}^{n_{i}}\\ C_{i}&=&B_{i}^{0}\leftarrow B_{i}^{1},\ldots,B_{i}^{k_{i}}\\ A_{i}^{j}\theta_{i}&=&B_{i}^{0}\theta_{i}\\ G_{i+1}&=&\leftarrow(A_{i}^{1},\ldots,A_{i}^{j-1},B_{i}^{1},\ldots,B_{i}^{k_{i% }},A_{i}^{j+1},\ldots,A_{i}^{n_{i}})\theta_{i}\end{array}

Observe como el lado derecho de $C_{i}$ reemplaza a la literal $A_{i}^{j}$ .
Una refutación SLD es una derivación SLD de $\square$ .
La regla para seleccionar una literal $A_{i}^{j}$ de una cláusula meta $G_{i}$ es la regla de cómputo.
La regla para escoger una cláusula $C_{i}\in P$ es la regla de búsqueda.

Ejemplo 2.7.

Sea $\leftarrow Q(y,b),Q(b,z)$ una cláusula meta para el programa en el Ejemplo 2.3. En cada paso debemos escoger una literal dentro de dicha cláusula meta y también una cláusula de programa cuya cabeza colisione con la literal seleccionada.

\begin{array}[]{lrr}11\mathchar 46\relax\leftarrow Q(y,b),Q(b,z)&&\text{\small cl% áusula meta}\\ 12\mathchar 46\relax\leftarrow P(y,b),Q(b,z)&&\text{\small tomando $Q(y,b)$, % Res 1, 11}\\ 13\mathchar 46\relax\leftarrow Q(b,z)&[y:=d]&\text{\small tomando $P(y,b)$, % Res 5, 12}\\ 14\mathchar 46\relax\leftarrow P(b,z)&&\text{\small tomando la única literal, % Res 1, 13}\\ 15\mathchar 46\relax\;\square&[z:=a]&\text{\small tomando la única literal, % Res 3, 14}\end{array}

Por lo tanto, tenemos una refutación para $\leftarrow Q(y,b),Q(b,z)$ bajo la sustitución $\theta=[y:=d,z:=a]$ . Como la resolución es correcta, concluimos que:

P\models\forall\big{(}\neg(\neg Q(y,b)\vee\neg Q(b,z))\theta\big{)}

de manera que $\theta$ es una sustitución de respuesta correcta, y $Q(d,b)\wedge Q(b,a)$ es verdadera para cualquier modelo de $P$ .

Definición 2.8.

A continuación se dan algunas definiciones para saber de donde proviene el término SLD para el tipo de resolución que estamos estudiando:

Resolución lineal.: Es una regla en la cual la resolución utiliza siempre la cláusula meta actual que se va generando.
La regla de cómputo o función de selección.: Se refiere a la regla que indica cual átomo de la meta se elige para aplicar resolución. En Prolog se elige la literal más a la izquierda de la cláusula meta.
Una cláusula definida: es de la forma $A\leftarrow B_{1},\ldots,B_{i}$ con $i\geq 0$ . Si $i=0$ , la cláusula es un hecho.
Resolución SLD: (Selected, linear, definite resolution) Resolución lineal con función de selección tomando cláusulas definidas.

Notemos que la resolución SLD es muy sensible a las reglas de cómputo y de búsqueda que se emplean. Puede que para un programa $P$ y una cláusula meta $G$ existan varias derivaciones produciendo distintas sustituciones de respuesta correcta; o, dependiendo de estas reglas, puede que la derivación entre en un ciclo y no termine, o bien, puede terminar con una falla al no poder realizar más pasos de la derivación.

Ejemplo 2.9.

Considere de nueva cuenta el programa en el Ejemplo 2.3. En el Ejemplo 2.7 se demostró que hay una refutación para la meta $\leftarrow Q(y,b),Q(b,z)$ con sustitución de respuesta correcta $\theta=[y:=d,z:=a]$ . Realice una refutación distinta para la misma meta obteniendo una sustitución de respuesta correcta diferente.

\begin{array}[]{lrr}11\mathchar 46\relax\leftarrow Q(y,b),Q(b,z)&&\text{\small cl% áusula meta}\\ 12\mathchar 46\relax\leftarrow P(y,b),Q(b,z)&&\text{Res 1, 11}\\ 13\mathchar 46\relax\leftarrow Q(b,z)&[y:=e]&\text{Res 6, 12}\\ 14\mathchar 46\relax\leftarrow P(b,z)&&\text{Res 1, 13}\\ 15\mathchar 46\relax\;\square&[z:=a]&\text{Res 3, 14}\end{array}

La refutación anterior produce la sustitución $[y:=e,z:=a]$ , por lo que puede haber más de una sustitución de respuesta correcta para una cláusula meta.

Ejemplo 2.10.

Suponga que la regla de cómputo toma la última literal en la cláusula meta, y que la regla de búsqueda escoge primero las cláusulas más abajo y luego las de arriba. Realice tres pasos de la refutación de la cláusula meta $\leftarrow Q(y,b),Q(b,z)$ .

\begin{array}[]{lrr}11\mathchar 46\relax\leftarrow Q(y,b),Q(b,z)&&\text{\small cl% áusula meta}\\ 12\mathchar 46\relax\leftarrow Q(y,b),P(b,z^{\prime}),Q(z^{\prime},z)&&\text{% Res 2, 11}\\ 13\mathchar 46\relax\leftarrow Q(y,b),P(b,z^{\prime}),P(z^{\prime},z^{\prime% \prime}),Q(z^{\prime\prime},z)&&\text{Res 2, 12}\\ 14\mathchar 46\relax\leftarrow Q(y,b),P(b,z^{\prime}),P(z^{\prime},z^{\prime% \prime}),P(z^{\prime\prime},z^{\prime\prime\prime}),Q(z^{\prime\prime\prime},z% )&&\text{Res 2, 13}\\ \qquad\qquad\qquad\qquad\vdots&&\vdots\end{array}

Ejemplo 2.11.

Si ahora suponemos que la regla de cómputo toma la primera literal en la cláusula meta, y la regla de búsqueda recorre las literales de abajo hacia arriba, podemos intentar la refutación de $\leftarrow Q(y,b),Q(b,z)$ del siguiente modo:

\begin{array}[]{lrr}11\mathchar 46\relax\leftarrow Q(y,b),Q(b,z)&&\text{\small cl% áusula meta}\\ 12\mathchar 46\relax\leftarrow P(y,z^{\prime}),Q(z^{\prime},b),Q(b,z)&&\text{% Res}\ 2,11\\ 13\mathchar 46\relax\leftarrow Q(b,b),Q(b,z)&[y:=j,z^{\prime}:=b]&\text{Res}\ % 10,12\\ 14\mathchar 46\relax\leftarrow P(b,z^{\prime\prime}),Q(z^{\prime\prime},b),Q(b% ,z)&&\text{Res}\ 2,13\\ 15\mathchar 46\relax\leftarrow Q(a,b),Q(b,z)&[z^{\prime\prime}:=a]&\text{Res}% \ 3,14\\ 16\mathchar 46\relax\leftarrow P(a,z^{\prime\prime\prime}),Q(z^{\prime\prime% \prime},b),Q(b,z)&&\text{Res}\ 2,15\\ 17\mathchar 46\relax\;???&&\end{array}

Aunque existe una sustitución de respuesta correcta como se ha visto previamente, esta refutación en particular ha fallado, ya que no hay cláusula de programa que pueda unificarse con $P(a,z^{\prime\prime\prime})$ .

Como se verá más adelante, Prolog toma la literal más a la izquierda de la meta y recorre las cláusulas de programa de arriba hacia abajo, hasta encontrar un cláusula con la cual realizar resolución. Si la refutación actual falla, Prolog regresa a un punto de retorno para intentar una refutación distinta con la misma literal más a la izquierda de la meta.

2.4 Teoremas de correctud y completud

Teorema 2.12 (Correctud de las resolución SLD).

Sea $P$ un conjunto de cláusulas de programa, $R$ una regla de cómputo y $G$ una cláusula meta. Suponga que hay una refutación SLD de $G$ . Sea $\theta=\theta_{1}\theta_{2}\ldots\theta_{n}$ la composición de los unificadores usados en la refutación y sea $\sigma$ la restricción de $\theta$ a las variables de $G$ . Entonces $\sigma$ es una sustitución de respuesta correcta para $G$ .

Demostración. Por definición de $\sigma$ , $G\theta=G\sigma$ , así que $P\cup\{G\sigma\}=P\cup\{G\theta\}$ , lo cual es insatisfacible porque la resolución es correcta. Pero que $P\cup\{G\sigma\}$ sea insatisfacible implica que $P\models\neg G\sigma$ . Como esto es cierto para cualquier sustitución en las variables libres de $G\sigma$ , se sigue que $P\models\forall(\neg G\sigma)$ , es decir, $\sigma$ es una sustitución de respuesta correcta para $G$ . $\blacksquare$

Teorema 2.13 (Completud de las resolución SLD).

Sea $P$ un conjunto de cláusulas de programa, $R$ una regla de cómputo, $G$ una cláusula meta y $\sigma$ una sustitución de respuesta correcta. Luego, hay una refutación SLD de $G$ a partir de $P$ tal que $\sigma$ es la restricción de la composición de los unificadores de $\theta_{1}\theta_{2}\ldots\theta_{n}$ a las variables de $G$ .

La refutación SLD es completa para cláusulas de Horn, pero no en general.

Ejemplo 2.14.

Consideremos el conjunto $S$ de cláusulas insatisfacibles:

\begin{array}[]{ll}1\mathchar 46\relax&p\lor q\\ 2\mathchar 46\relax&\neg p\lor q\\ 3\mathchar 46\relax&p\lor\neg q\\ 4\mathchar 46\relax&\neg p\lor\neg q\\ \end{array}

$S$ no es un conjunto de cláusulas de Horn puesto que $p\lor q$ tiene dos literales positivas. Aunque $S$ tiene una refutación por resolución general, ya que es insatisfacible y la resolución es completa:

\begin{array}[]{lll}5\mathchar 46\relax&q&\text{Res 1, 2}\\ 6\mathchar 46\relax&\neg q&\text{Res 3, 4}\\ 7\mathchar 46\relax&\Box&\text{Res 5, 6}\end{array}

Esta no es una refutación SLD porque el paso final resuelve dos cláusulas meta, no una cláusula meta con una de las cláusulas del programa en $S$ .

Refutaciones como cómputos

Dado un programa y una consulta expresada como una cláusula meta, el resultado de una refutación exitosa es una respuesta obtenida de las sustituciones llevadas a cabo por la unificación. En lenguajes de programación, el control del cómputo se construye explícitamente por el programador, quien puede ocupar estructuras de control como:

if(...) ... else ...

for(...) ...

En programación lógica, el programador escribe fórmulas declarativas que describen la relación entre la entrada y la salida. El motor de inferencia de la resolución provee una estructura de control implícita uniforme, así que se mitiga la tarea del programador de especificar el control explícitamente. Los lenguajes de programación lógicos permiten abstraer la estructura de control. Dicho control depende fuertemente de las reglas de cómputo y de búsqueda.

2.5 Árbol SLD

El conjunto de derivaciones SLD para un programa lógico puede ser visto como un árbol.

Definición 2.15.

Sea $P$ un conjunto de cláusulas de programa, $R$ una regla de cómputo y $G$ una cláusula meta. Un árbol SLD se genera del siguiente modo: La raíz se etiqueta con la cláusula meta $G$ . Dado un nodo $n$ etiquetado con un cláusula meta $G_{n}$ , se produce un hijo $n_{i}$ por cada cláusula meta nueva $G_{n_{i}}$ que se obtiene al resolver la literal escogida por $R$ con la cabeza de una cláusula en $P$ .

Ejemplo 2.16.

La Fig. 1 muestra un árbol SLD para la cláusulas de programa en el Ejercicio 2.3 y la cláusula meta $\leftarrow Q(y,b)$ . La regla de cómputo escoge siempre la literal más a la izquierda en la cláusula meta, la cual está subrayada. El número en la arista se refiere al número de la cláusula de programa que colisionó con la cláusula meta.

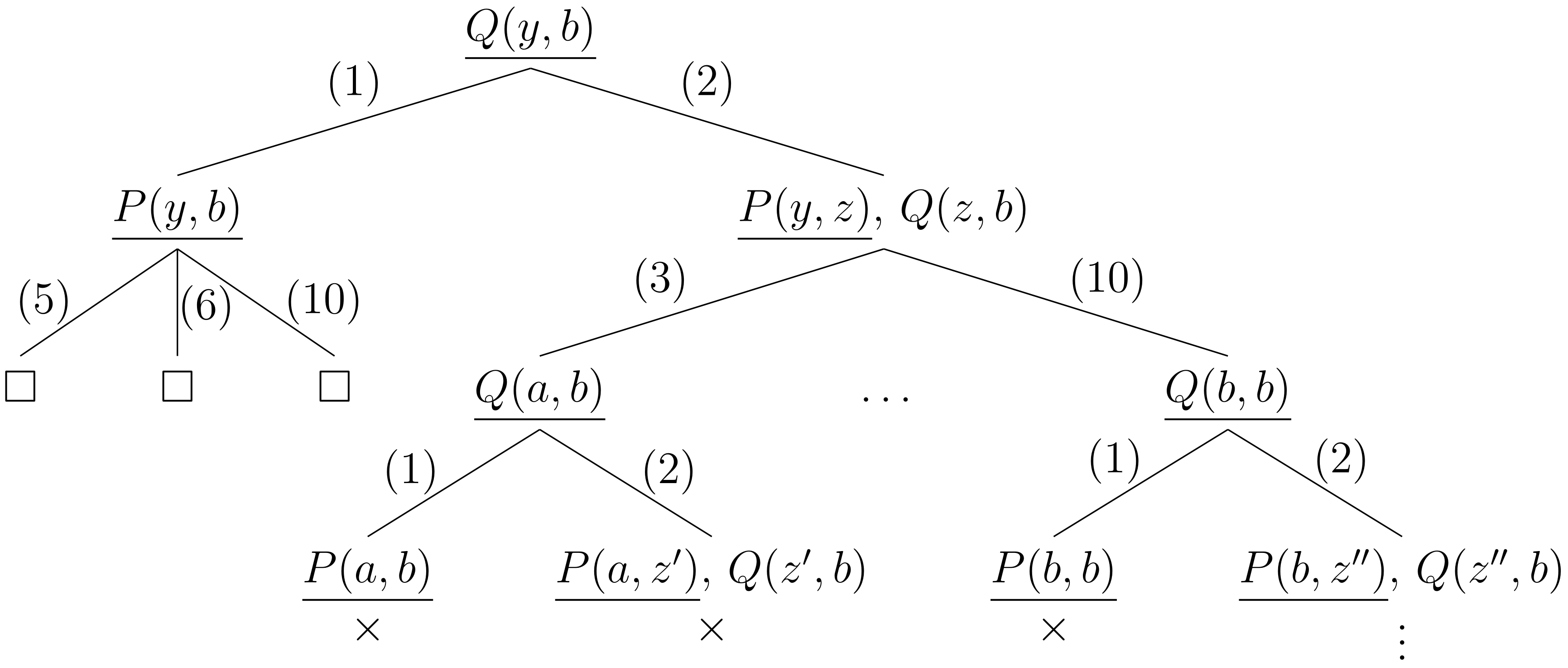
Figura 1: Árbol SLD que selecciona la literal más a la izquierda.

Definición 2.17.

En un árbol SLD, una rama que conduce a una refutación es una rama de éxito. Una que lleva a una cláusula meta cuya literal seleccionada no unifica con ninguna cláusula de programa es una rama de fallo. Una rama que corresponda a una derivación que no termina es una rama infinita.

Puede ser que haya muchos árboles SLD, uno para cada regla de cómputo; sin embargo, el siguiente teorema nos dice que todos los árboles que se obtienen son similares.

Teorema 2.18.

Sea $P$ un programa y $G$ una cláusula meta. Entonces todos los árboles SLD para $P$ y $G$ tienen un número infinito de ramas de éxito o tienen todos el mismo número finito de ramas de éxito.

Definición 2.19.

Una regla de búsqueda es un procedimiento para buscar una refutación en un árbol SLD. Un procedimiento de refutación SLD es el algoritmo de resolución SLD junto con la especificación de una regla de cómputo y una regla de búsqueda.

La resolución SLD es completa independientemente de la regla de cómputo, pero solo afirma la existencia de una refutación. La regla de búsqueda determinará si se encuentra o no la refutación, y qué tan eficiente es el procedimiento. Una búsqueda por amplitud de un árbol SLD, donde se revisan los nodos a cada nivel antes de buscar más profundamente, garantiza encontrar una rama de éxito si es que la hay. En cambio, una búsqueda a profundidad puede elegir recorrer una rama que no termina. En la práctica, se prefiere la búsqueda a profundidad porque necesita mucha menos memoria: una pila del camino que se está explorando, donde cada elemento registra qué rama se tomó en cada nodo y las sustituciones que se realizaron en ese nodo. En una búsqueda por amplitud, esta información debe almacenarse para todas las hojas en el nivel actual de la búsqueda.

Definición 2.20.

Un árbol de prueba por refutación basado en resolución SLD es un árbol binario (aunque su forma es lineal) con nodos etiquetados con cláusulas meta o cláusulas de programa, construido mediante aplicaciones de la regla de resolución binaria del siguiente modo: si $C_{R}$ es una cláusula resolvente a partir de la cláusula de programa $C$ , la cláusula meta $G$ y la regla de cómputo $R$ , entonces el árbol tendrá a $C_{R}$ como hijo de $C$ y de $G$ . Este procedimiento se repite tomando ahora a $C_{R}$ como la nueva cláusula meta, y termina cuando $C_{R}=\square$ .

La Fig. 2 muestra el árbol de prueba por refutación basado en resolución SLD obtenido a partir del Ejemplo 2.7.

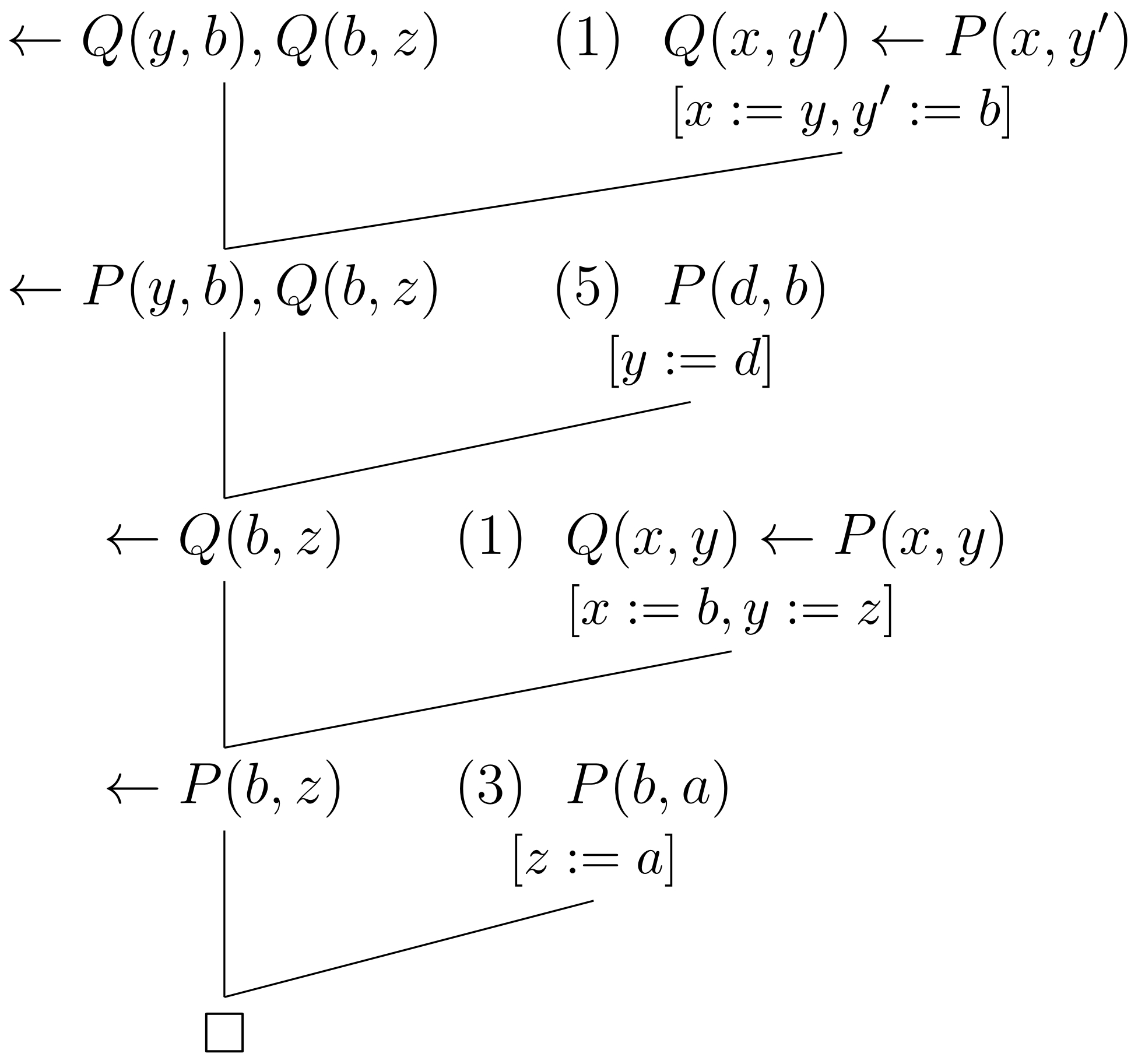
Figura 2: Árbol de prueba por refutación basado en resolución SLD. Como se aprecia, el árbol es lineal. A la izquierda están las cláusulas meta. A la derecha las cláusulas de programa y su número correspondiente entre paréntesis, abajo el unificador más general para efectuar un paso de resolución.

3 Prolog

Prolog fue el primer lenguaje de programación lógica. La regla de cómputo en Prolog escoge la literal más a la izquierda. La regla de búsqueda toma cláusulas de arriba hacia abajo. La notación en Prolog difiere de la notación matemática que hemos usado:

a)

las variables inician con letras mayúsculas,
b)

los predicados inician con letras minúsculas,
c)

todas las declaraciones terminan con un punto (.), y
d)

el símbolo :- se usa en lugar de $\leftarrow$ .

Ejemplo 3.1.

Reescribamos el programa del Ejemplo 2.3 usando la notación de Prolog .

ancestro(X,Y) :- progenitor(X,Y).
ancestro(X,Y) :- progenitor(X,Z),ancestro(Z,Y).

progenitor(bob, allen).
progenitor(catherine, allen).
progenitor(dave, bob).
progenitor(ellen, bob).
progenitor(fred, harry).
progenitor(harry, george).
progenitor(ida, george).
progenitor(joe, bob).

Usamos progenitor cuando hablamos de la relación ser papá o mamá. El procedimiento para ancestro da un significado declarativo de este concepto en términos de la relación progenitor:

X es un ancestro de Y si X es un progenitor de Y.
X es un ancestro de Y si hay Z tal que X es un progenitor de Z, Z es un ancestro de Y.

3.1 Búsqueda a profundidad

La búsqueda en un árbol SLD generado por Prolog sigue una búsqueda a profundidad, lo que puede originar la no terminación de un cómputo, incluso si existe un cómputo que en efecto termina. Un programador de Prolog debe ordenar cuidadosamente las cláusulas dentro de un procedimiento y las literales dentro de las cláusulas para evitar que la ejecución no termine. Considere los siguientes dos programas en Prolog :

test :- p(X).

p(a).

p(X) :- p(f(X)).

test :- p(X).

p(X) :- p(f(X)).

p(a).

Al realizar la consulta ?-test. el programa de la izquierda terminará en el segundo paso de la resolución, mientras que el de la derecha efectuará la resolución con p(X) :- p(f(X)). en cada paso de la derivación y nunca terminará. De aquí la importancia de acomodar bien las cláusulas en el programa.

Como una falla puede ocurrir en cualquier paso, Prolog almacena una lista de puntos de retorno²²Backtrack points.. Estos puntos representan nodos previos en el árbol SLD donde existen ramas adicionales por explorar.

Un concepto importante al programar en Prolog es el forzar la falla. Esto se implementa por el predicado fail. En esencia, una vez llegado el predicado fail se obliga a regresar al punto de retorno inmediato anterior. Prolog carece de estructuras iterativas tales como los ciclos for y while, así que la recursión y el forzar la falla son técnicas de programación fundamentales en este lenguaje. Por ejemplo, si al programa en Prolog del Ejemplo 3.1 le damos la cláusula meta ?- ancestro(Y,bob),ancestro(bob,Z),format("Y: ~w, Z: ~w\n", [Y,Z]),fail. se imprime en pantalla lo siguiente

Y: dave, Z: allen
Y: ellen, Z: allen
Y: fred, Z: allen
false.

3.2 Prolog y la teoría de programación lógica

Predicados no lógicos

Los predicados no lógicos son predicados cuyo propósito principal es generar efectos secundarios. El ejemplo obvio son los predicados de entrada y salida (I/O), como read, write y print, que no tienen significado declarativo como fórmulas lógicas.

Aritmética

Prolog deja la programación lógica teórica en su tratamiento de tipos de datos numéricos. Aunque es posible formalizar la aritmética en lógica de primer orden, hay dos problemas con este formalismo. Primero, sería algo incómodo, por ejemplo, al ejecutar una consulta sobre el número de empleados en una tienda departamental y recibir como respuesta el término $f(f(f(f(f(a)))))$ en lugar de 5. El segundo problema es la ineficiencia de la resolución como método de computación numérica.

Prolog soporta la aritmética estándar. La sintaxis es la de un predicado con un operador infijo, a saber, Result is Expression. La siguiente cláusula obtiene el precio de lista y el descuento de una base de datos, y calcula el valor del Precio después de aplicarle el descuento:

precio_de_venta(Articulo, Precio):-
   precio_de_lista(Articulo, Lista),
   porcentaje_descuento(Articulo, Descuento),
   Precio is Lista - Lista * Descuento / 100.

Los predicados aritméticos difieren de los predicados ordinarios porque son de ida únicamente, no como lo es la unificación. Si 10 is X+Y, X y Y podrían ser unificados con 0 y 10, y al tomar puntos de retorno, podrían ser unificados con 1 y 9, y así sucesivamente. Sin embargo, esto es ilegal. En Result is Expression, Expression debe ser evaluada a un valor numérico, entonces dicho valor es unificado con Result (quien es típicamente una variable que no se ha instanciado).

Los predicados aritméticos no son enunciados de asignación. El siguiente programa no es correcto:

precio_de_venta(Articulo, Precio):-
   precio_de_lista(Articulo, Lista),
   porcentaje_descuento(Articulo, Descuento),
   Precio is Lista - Lista * Descuento / 100,
   porcentaje_iva(Articulo, Impuesto),
   Precio is Precio * (1 +  Impuesto / 100).

Una vez que Precio ha sido unificado cualquier intento de unificarlo una vez más fallará, justo como una variable $x$ en una fórmula lógica no puede ser modificada una vez que una sustitución por una constante tal como $[x:=a]$ se ha aplicado. Una variable adicional debe ser usada para guardar el valor intermedio.

precio_de_venta(Articulo, Precio):-
   precio_de_lista(Articulo, Lista),
   porcentaje_descuento(Articulo, Descuento),
   Precio1 is Lista - Lista * Descuento / 100,
   porcentaje_iva(Articulo, Impuesto),
   Precio is Precio1 * (1 +  Impuesto / 100).

Cut

La modificación más controversial a la programación lógica introducida en Prolog es el corte (cut). Considere el siguiente programa para calcular el factorial de un número $N$ :

factorial(0, 1).
factorial(N, F):-
  N1 is N-1,
  factorial(N1, F1),
  F is N*F1.

Esta es una traducción a Prolog de la fórmula recursiva:

f(0)=1,\qquad f(n)=n\cdot f(n-1)\mathchar 46\relax

Ahora, supongamos que el resultado de este predicado es parte de otro procedimiento, tal vez uno que verifique una propiedad de números que son factoriales:

check(N) :- factorial(N, F), property(F).

Si check es invocado con N=0, llamará a factorial(0, F) lo que devolverá F=1 y llamará a property(1). Suponga que la llamada a este último predicado falla. Entonces el procedimiento de resolución SLD volverá a un punto de retorno, deshará la sustitución F=1, y lo intentará con la segunda cláusula en el procedimiento para factorial. La llamada recursiva a factorial(-1, F1) iniciará un cómputo que no terminará. Prolog imprimirá en pantalla ERROR: Out of local stack.

Digamos que property(X) verifica que X es un número par. Su declaración en Prolog es la siguiente:

property(X):-
   M is mod(X,2),
   M == 0.

Ponemos en el intérprete de Prolog el comando trace. que permite dar seguimiento a las llamadas de programa que se efectúan. Así, al tener la consulta [trace] ?- check(0). obtenemos en pantalla:

   Call: (8) check(0) ? creep
   Call: (9) factorial(0, _3746) ? creep
   Exit: (9) factorial(0, 1) ? creep
   Call: (9) property(1) ? creep
   Call: (10) _3750 is 1 mod 2 ? creep
   Exit: (10) 1 is 1 mod 2 ? creep
   Call: (10) 1==0 ? creep
   Fail: (10) 1==0 ? creep
   Fail: (9) property(1) ? creep
   Redo: (9) factorial(0, _3746) ? creep
   Call: (10) _3750 is 0+ -1 ? creep
   Exit: (10) -1 is 0+ -1 ? Unknown option (h for help)
   Exit: (10) -1 is 0+ -1 ? Unknown option (h for help)
   Exit: (10) -1 is 0+ -1 ? Show context
   .
   .
   .

Se realizaran un número indefinido de llamadas a la segunda cláusula de factorial, y el stack se acabará sin terminar el cómputo.

Una llamada a factorial con argumento 0 tiene una única solución; si volvemos a puntos de retorno, la cláusula meta fallará. Esto puede ser evitado introduciendo un corte, denotado por un símbolo de exclamación, al final de la primer cláusula:

factorial(0, 1):- !.

El corte impide volver a puntos de retorno en este procedimiento. Una vez que el corte se ejecuta se tala una porción del árbol SLD e impide volver a puntos de retorno que no conviene explorar.

En el caso del factorial hay una mejor solución, a saber, agregar un predicado al cuerpo del procedimiento que explícitamente prevenga el comportamiento indeseado.

factorial(0, 1).
factorial(N, F):-
  N > 0,
  N1 is N-1,
  factorial(N1, F1),
  F is N*F1.

Finalmente, considere el siguiente ejemplo de programación lógica en Prolog , donde el predicado take_even(X,Y) establece que en la lista Y figuran los elementos pares de X, por ejemplo, take_even([-5,-2,1,2,6,7],[-2,2,6]). Su definición es:

take_even([],[]).
take_even([H|T],[H|T1]):-
  is_even(H),
  take_even(T,T1),!.
take_even([_|T],T1):-
  take_even(T,T1).

is_even(X):-
   M is mod(X,2),
   M == 0.

Hemos usado la variable anónima, denotada _ (guión bajo), en la definición de take_even([_|T],T1), ya que se está analizando el caso en el que la cabeza de la primer lista no es par, como dicho elemento no tiene importancia y no se hace referencia a él en ningún otro lado, se representa como una variable anónima.

Lógica Computacional Nota 12. Resolución SLD y programación lógica11Esta nota se base en material elaborado por el prof. Favio Miranda y en el libro de Ben-Ari M., Mathematical Logic for Computer Science