Clustering, reducción dimensional y visualización
Sin supervisión
De una colección de datos, agruparlos
K-means
Algoritmo más popular para clustering
Tiene como parámetros el número $k$ de clusters
Suposiciones
- Distancia entre ejemplos
- Espacio Euclidiano
Formulación
Para $X=x_1,\ldots, x_n \in \mathcal{R}^D$, para todas las $k$ particiones $\mathcal{P}=C_1\cap C_2 \cap \ldots \cap C_k$
$$ \mathop{\textrm{min}}_{c_1 \cup \ldots \cup c_k} \sum_{i=1}^k \sum_{x_i\in C_i} \left\lvert x - \frac{1}{C_i}\sum_{x_j \in C_i}x_j \right\lvert^2 $$NP-hard 😢
Algoritmo
- Inicializar $k$ media más cercana con 4 puntos aleatorios de $X$
- Asignar cada punto de $X$ a la media más cercana
- Calcular una nueva media basada en la asignación
- Si convergió, finalizar, caso contrario, regresar a $2$
Sólo converge a mínima local
Versiones
- Lloyd, 1957, Algoritmo k-means
- Vassilvitskii, 2007, k-means++, mejor inicialización
- Kummar, 2010, Todavía mejor inicialización
Evaluación
Truculento porque no hay salida
Error cuadrático
$$ \mathop{\textrm{min}}_{c_1 \cup \ldots \cup c_k} \sum_{i=1}^k \sum_{x_i\in C_i} \left\lvert x_i - \mu_k \right\lvert^2 $$Pureza
Cada cluster se asigna a la clase con mayor datos, y se calcula accuracy
Múltiples métricas
adjusted multual information, adjusted rand, Calinski-Harabaz, completud, Fowlkes-Mallows, Homogeneidad, silueta, ...
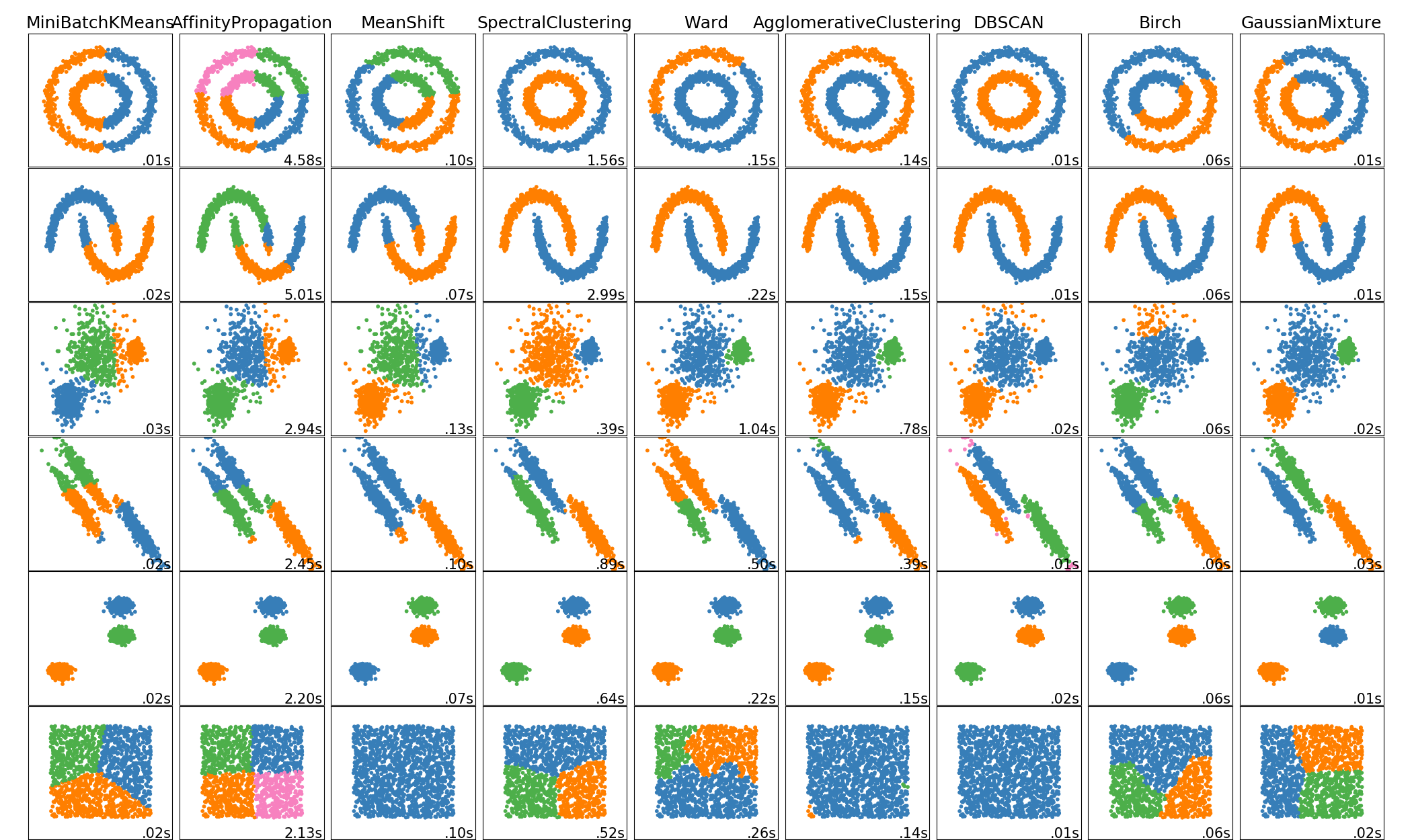
Reducción dimensional
Reducir el número de dimensiones
Formalmente
Dado un dataset $\mathbf{D}$ tal qué $\mathbf{D_i} \in \mathcal{R}^n$
$$ \mathbf{D} \rightarrow \mathbf{\hat{D}} \text{ tal qué } \mathbf{\hat{D}_i} \in \mathcal{R}^k \\\text{ donde } k \lt n $$
Opciones
Eliminar columnas
- Aquellas que no tienen muchos valores
- Aquellas que tienen poca varianza
- Aquellas con alta correlación (Correlación person)
Más opciones
Basado en el método
- Eliminar malos "features"
- Agregar buenos "features"
Principal Component Analysis
Análisis de componentes principales
Lo qué queremos
Transformar nuestros vectores a vectores
$$ Ax = \hat{x} $$Concepto básico
$$\left[ \begin{array} a a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mm} \\ \end{array} \right] \left[ \begin{array}x x_1 \\ x_2 \\ \vdots \\ x_m \end{array}\right] = \left[ \begin{array}x \hat{x}_1 \\ \hat{x}_2 \\ \vdots \\ \hat{x}_m \end{array}\right] $$
$$ (m\times m) (m\times 1) = m \times 1 $$
Sino tan cuadrada
$$\left[ \begin{array} a a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{k1} & a_{k2} & \cdots & a_{km} \\ \end{array} \right] \left[ \begin{array}x x_1 \\ x_2 \\ \vdots \\ x_m \end{array}\right] = \left[ \begin{array}x \hat{x}_1 \\ \hat{x}_2 \\ \vdots \\ \hat{x}_k \end{array}\right] $$
$$ (k\times m) (m\times 1) = k \times 1 $$
¿Qué propiedad necesitamos?
Qué implica "Aquellas que tienen poca varianza"
Aquella que deja la mayor parte de varianza
La proyección que guarda la mayor varianza
Formalmente
$$ \mathop{\textrm{max}}_{||v||=1} var(proj_vD) $$Una proyección es una transformación, pero el vector tiene menor dimensión
Un atájo
La transformación sin proyección
Es decir la transformación, que conserve la mayor varianza de los datos
Otro atajo
La matriz de covarianza
$$ cov(\mathbf{D}) = \sum_{i=0}^n x_i^T x_i$$si $\mu = 0$
Preprocesamiento de D
Quitar la media
$$ x_i = x_i-\mu $$La covarianza
¿Qué codifica?
$$ cov(\mathbf{D}) = \sum_{i=0}^n x_i^T x_i$$$$ m \times m $$
La varianza condicional, es triangular
Gira y escala los vectores hacia las dirección de mayor varianza
Último atajo
Eigenvectores de $cov(D)$
$$ v_1, v_2, \ldots, v_m \in \mathcal{R}^m$$Ahora si último atajo
Single Value Descomposition (SVD)
$$ M = U\times S \times V'$$Donde $U$ son los eigenvectores
En resumen (algoritmo PCA)
- Quitar la media de $\mathbf{D}$ (escalar opcional)
- Calcular $cov(\mathbf{D})$
- Calcular $U$ usando $SVD(cov(\mathbf{D}))$
- Cortar $U[:,:k]$ que llamamos $\hat{U}$
- Para cada valor de $\mathbf{D}$ calcular $\hat{U}^Tx_i$
Visulaizar con PCA
Reducir los puntos del dataset a dos dimensiones y graficar
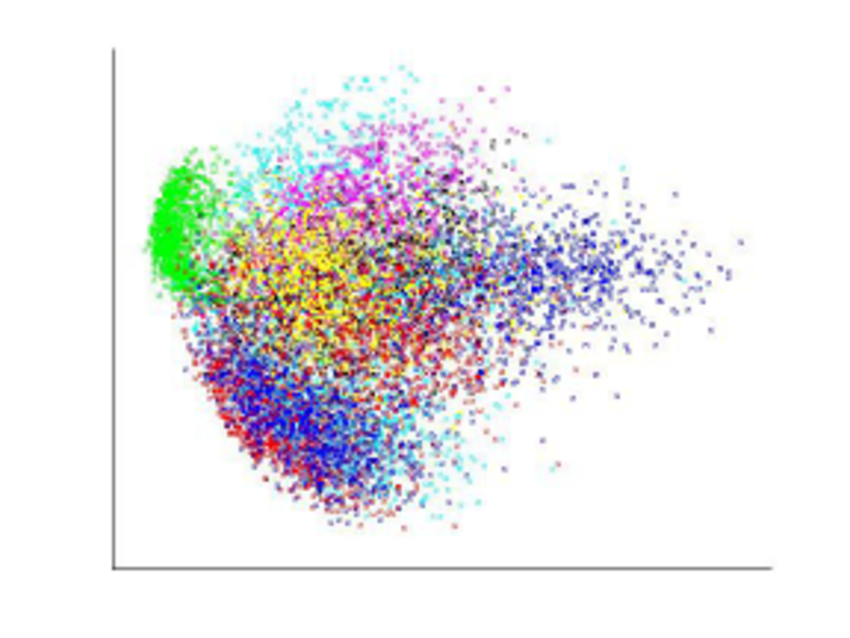
Como se maximiza la varianza, puntos muy distintos conservan su distancia
Se puede ver como minimizar el error cuadrático entre distancias entre puntos originales y puntos en el mapa (mayor peso a dejar las distancias largas del original)
¿Es lo que queremos?
t-SNE
Preservar las distancias locales
Formalmente
$$ p_{j|i} = \frac{\exp\left(-\left| x_i - x_j\right|^2 \big/ 2\sigma_i^2\right)}{\displaystyle\sum_{k \neq i} \exp\left(-\left| x_i - x_k\right|^2 \big/ 2\sigma_i^2\right)} $$
Para mayor

Clustering, reducción dimensional y visualización by Ivan V. Meza Ruiz is licensed under a Creative Commons Reconocimiento 4.0 Internacional License.
Creado a partir de la obra en http://turing.iimas.unam.mx/~ivanvladimir/slides/rpyaa/07_cluster.html.