• ivanvladimir@gmail.com
  • ivanvladimir
  • turing.iimas.unam.mx/~ivanvladimir

    • Redes Neuronales






    Ivan Meza


    El perceptrón (una neurona)



    • Inspirada en la redes neuronales naturales
    • Una neurona recibe señales de entrada
    • Que la activan o inhiben
    $$ y= f(w_1x_1+w_2x_2+\ldots+w_nx_n) $$
    • Sigmoide $[0 \ldots 1]$ $$ \frac{1}{1+e^{-x}} $$

    • Tangente hiperbólica $[-1 \dots 1]$ $$ \frac{e^x-e^{-x}}{e^x+e^{-x}} $$

    • ReLu (Rectifier Linear Unit) $[0 \dots \infty]$ $$ max(0,x) $$

    Sigmoide

    $$ y = \frac{1}{1+e^{-(w_1x_1+w_2x_2+\ldots+w_nx_n)}}$$

    ¿Qué le falta para ser regresión logística?

    Revisando

    $$ y= f(w_1x_1+w_2x_2+\ldots+w_nx_n+b) $$

    Re-escribiendo

    Como vectores

    $$ y= f(wx^T+b)\\ 1\times 1=(1\times n)(n \times 1) $$

    ¿Cómo entrenar?

    • Similar a distribución Gausiana
    • Descenso por gradiente

    Perceptrón multi-capa

    Varias cosas pasando

    • Entrada de dimensión del tipo $x \in \mathbf{R}^n$
    • se conecta a la primera capa de $m$ neuronas
    • esta conecta a la segunda capa de $o$ neuronas
    • esta genera la salida $y \in \mathbf{R}^o$
    • $x$ es vector de entrada
    • $W^1$ es la matrix de pesos, $m \times n$: unidades ocultas $\times$ entradas
    • $b^1$ es el vector de sesgo, de tamaño $m$
    • $h^1$ es el vector de salida de la primera capa

    Primera capa

    • $h^1=f^1(W^1x+b^1)$

    Estos valores son la entrada para la siguiente capa...

    Toda la red

    • $h^1=f^1(W^1x+b^1)$
    • $y=f^2(W^2h^1+b^2)$

    Más capas

    • $h^1=f^1(W^1x+b^1)$
    • $h^2=f^2(W^2h^1+b^2)$
    • $h^3=f^2(W^3h^2+b^3)$
    • $\cdots$
    • $y=f^m(W^mh^{(m-1)}+b^m)$

    Propagación de los pesos

    ¿Pesos...

    ... y sesgo?

    Gradient descent

    Error de dataset:

    $$ E(a^L,y) = \frac{1}{2n}\sum_{i=0}^n (a^L_i - y_i)^2 $$

    donde $a^L=f^m(W^mh^{(m-1)}+b^m)$

    Recordemos

    $\hat{\theta}=\theta-k \nabla E(a^L,y) $

    ¿Cuáles son los parámetros?

    $W$ y $b$

    Gradiente

    $$ \nabla = (\frac{\partial E}{\partial w^l_{jk}},\frac{\partial E}{\partial b^l_j}) $$

    Error neuron

    $$ \delta^l_j = \frac{\partial E}{\partial h^l_j} $$

    Ecuación 1: error última capa

    $$ \delta^L_j = \frac{\partial E}{\partial a^L_j}f'^L(h^L_j) $$

    Dónde para error cuadrático

    $$ \frac{\partial E}{\partial a^L_j}= (a^L_j-y_j) $$

    Re-escribiendo: vector

    $$ \delta^L = (a^L-y) \bigodot f'^L(h^L) $$

    Ecuación 2: error capa anterior

    $$ \delta^l = ((W^{l+1})^T\delta^{l+1}) \bigodot f'^l(h^l) $$

    Ecuación 3: error en bias

    $$ \frac{\partial E}{\partial b^l} = \delta^l $$

    Ecuación 4: error en bias

    $$ \frac{\partial E}{\partial w^l_{j,k}} = a^{l-1}_k\delta^l_j $$

    Retropropagación

    1. Calcular los valores de $h^l$ y $a_l$, propagación de pesos
    2. Calcular el error de la última capa $\delta^L$
    3. Retropropagar el error $\delta^l$
    4. Calcular los gradientes

    Deep learning

    1. Multiples capas
    2. Trucos para entrenar: batches (tensores), dropout, autograd
    3. Nuevas funciones de costo

    Taken from An overview of gradient descent optimization algorithms

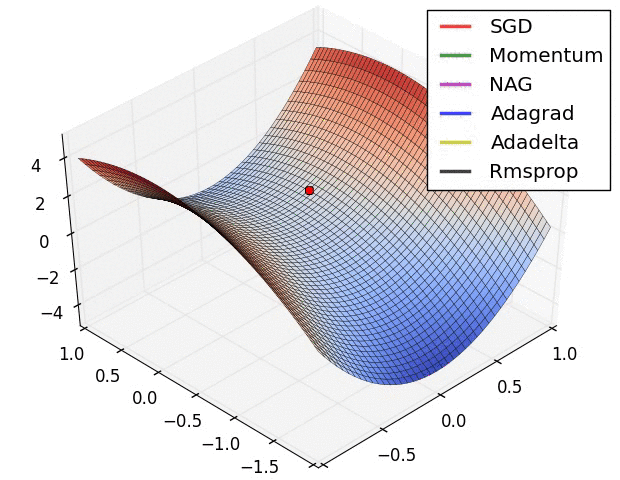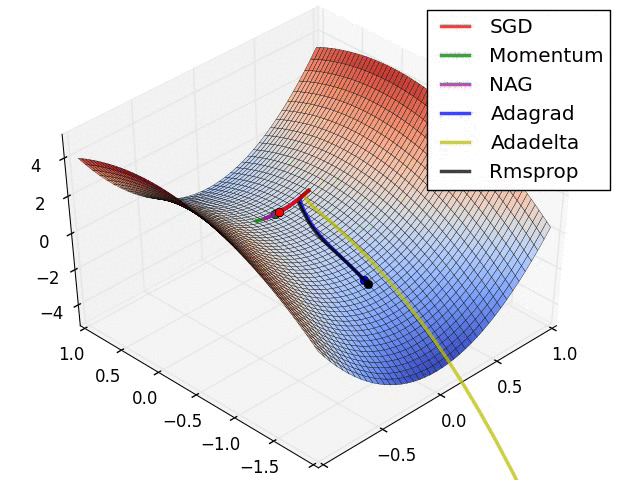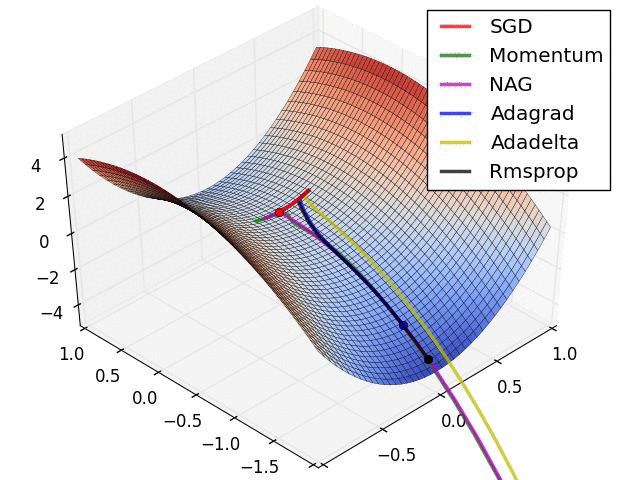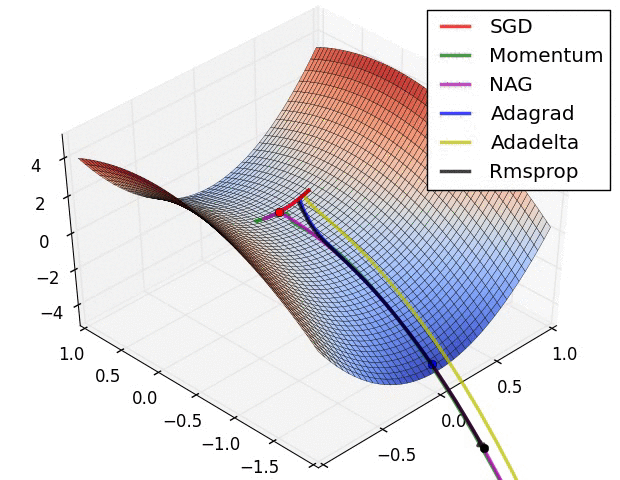
    Taken from An overview of gradient descent optimization algorithms

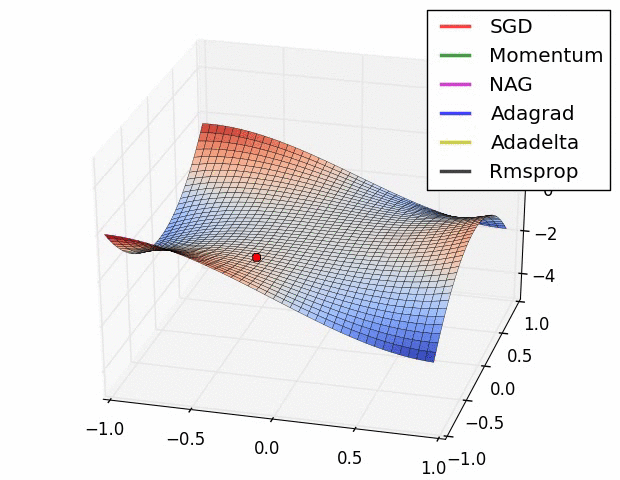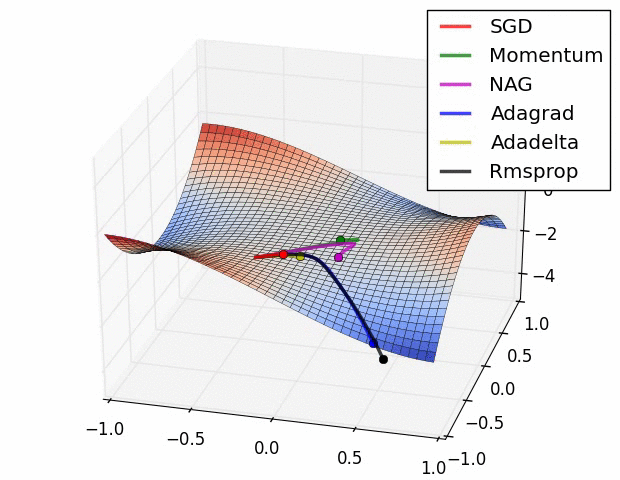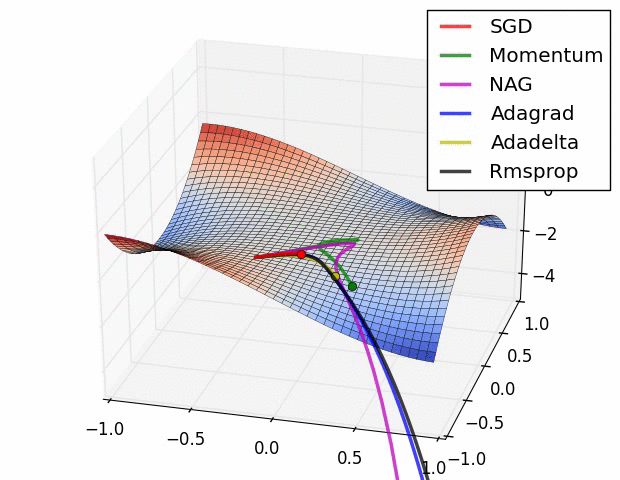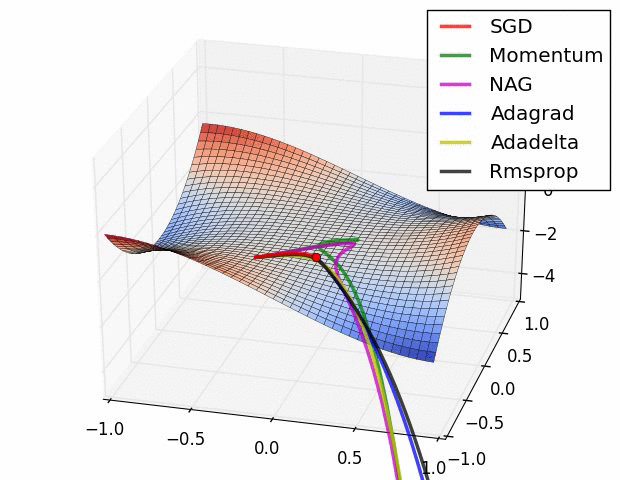
    Taken from Deep Learning in a Nutshell: History and Training

    Licencia de Creative Commons
    Neuronal Networks by Ivan V. Meza Ruiz is licensed under a Creative Commons Reconocimiento 4.0 Internacional License.
    Creado a partir de la obra en http://turing.iimas.unam.mx/~ivanvladimir/slides/rpyaa/09_nn.html.