Lógica Computacional
Nota 09. Tableaux semánticos para la lógica de predicados

1 Tableaux semánticos

El método de tableaux semánticos es un método de demostración por refutación. Antes de presentar las formalidades de este método, vamos a construir algunos tableaux informalmente para mostrar las dificultades que debemos afrontar y como se motivan sus soluciones, para esto necesitamos de la siguiente definición.

Definición 1.1.

Un término cerrado es un término que no tiene variables. Por ejemplo, $0$, $f(0)$, $f(f(0))$, $c$ y $h(a,f(b))$ son términos cerrados; mientras que $x$, $g(y,z)$ y $h(x,a)$ no lo son.

1.1 Ejemplos de Tableaux Semánticos

Instanciar fórmulas universales con los términos cerrados

Consideremos la fórmula válida:

$$\psi =\forall x(P(x)\to Q(x))\to (\forall xP(x)\to \forall xQ(x)),$$

y construyamos un tableaux para su negación.

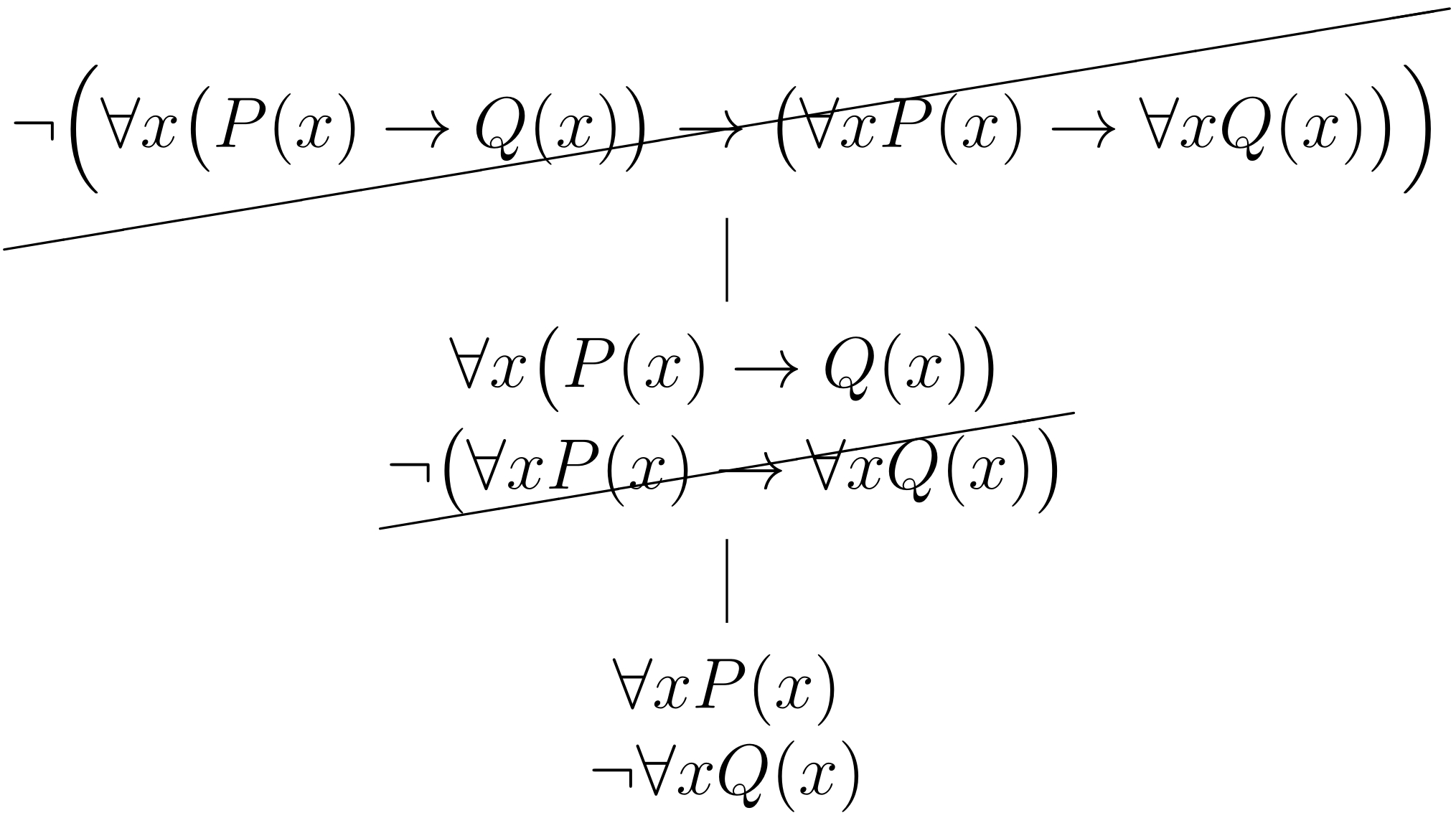
El enunciado $\neg \forall xQ(x)$ será verdadero en un modelo $ℳ$ solo si existe un elemento en el dominio $c$ tal que $c\notin Q^{ℳ}$. Usemos la primera constante $a_1$ para representar este elemento e instanciamos la fórmula con ella:

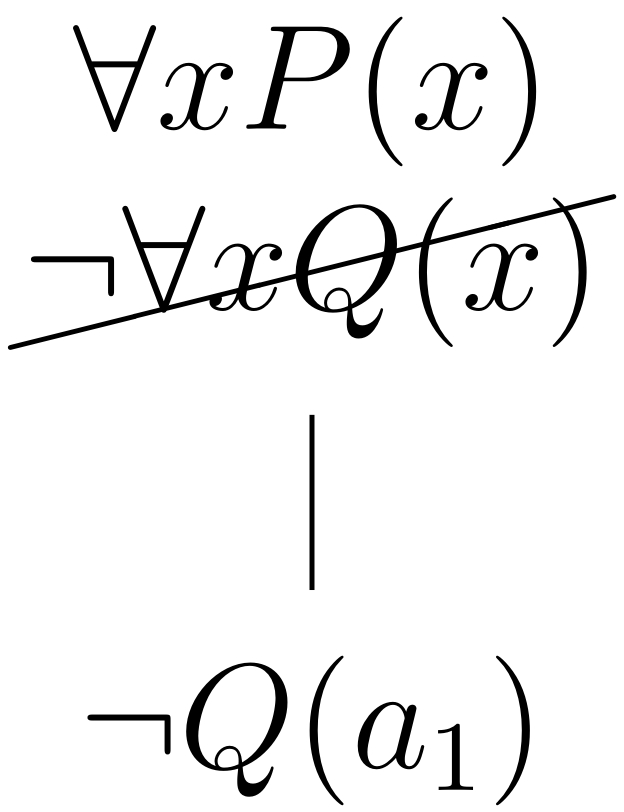
Como las fórmulas $\forall xP(x)$ y $\forall x\left(P(x)\to Q(x)\right)$ están cuantificadas universalmente, deben ser verdaderas para todo elemento del universo. Instanciamos estas fórmulas con la constante $a_1$:

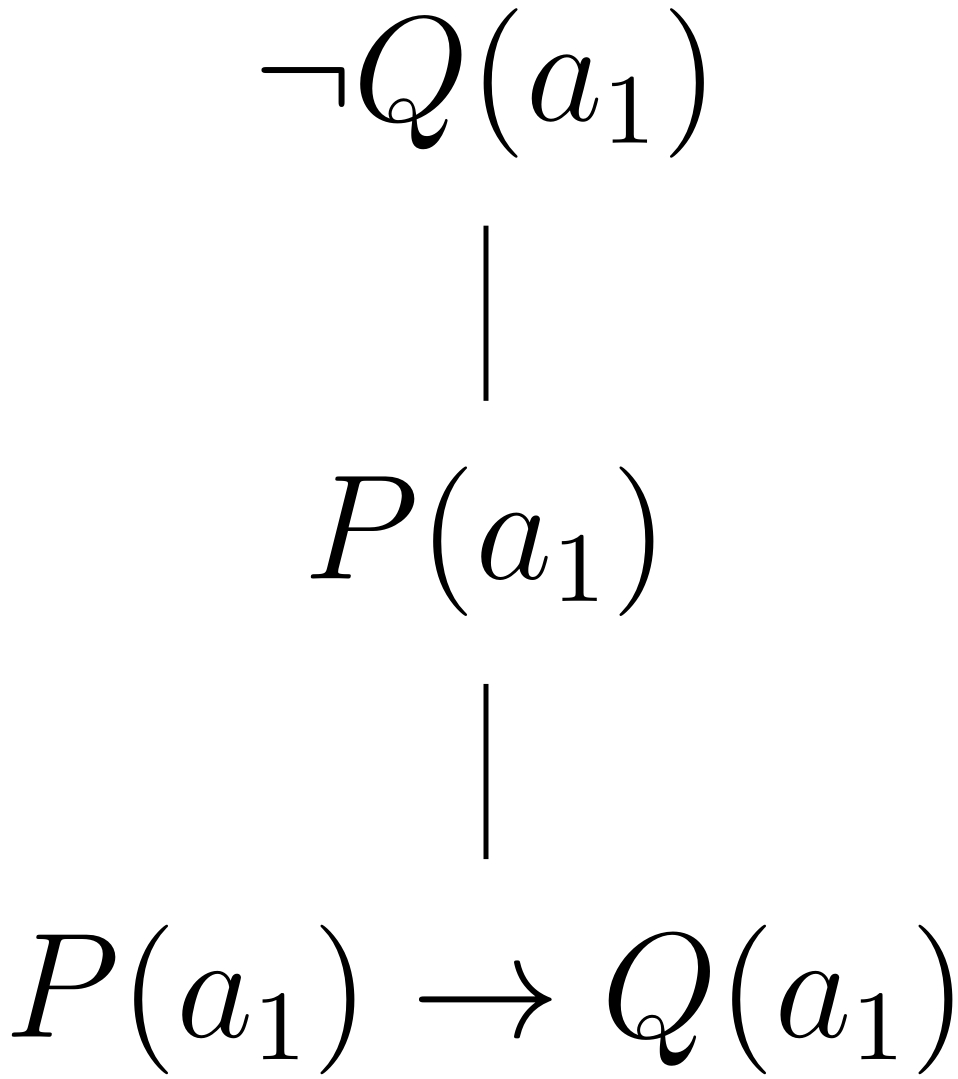
Aplicando la regla $\beta$ a la fórmula $P(a_1)\to Q(a_1)$, obtenemos inmediatamente un tableaux cerrado, como era de esperarse para la negación de una fórmula válida.

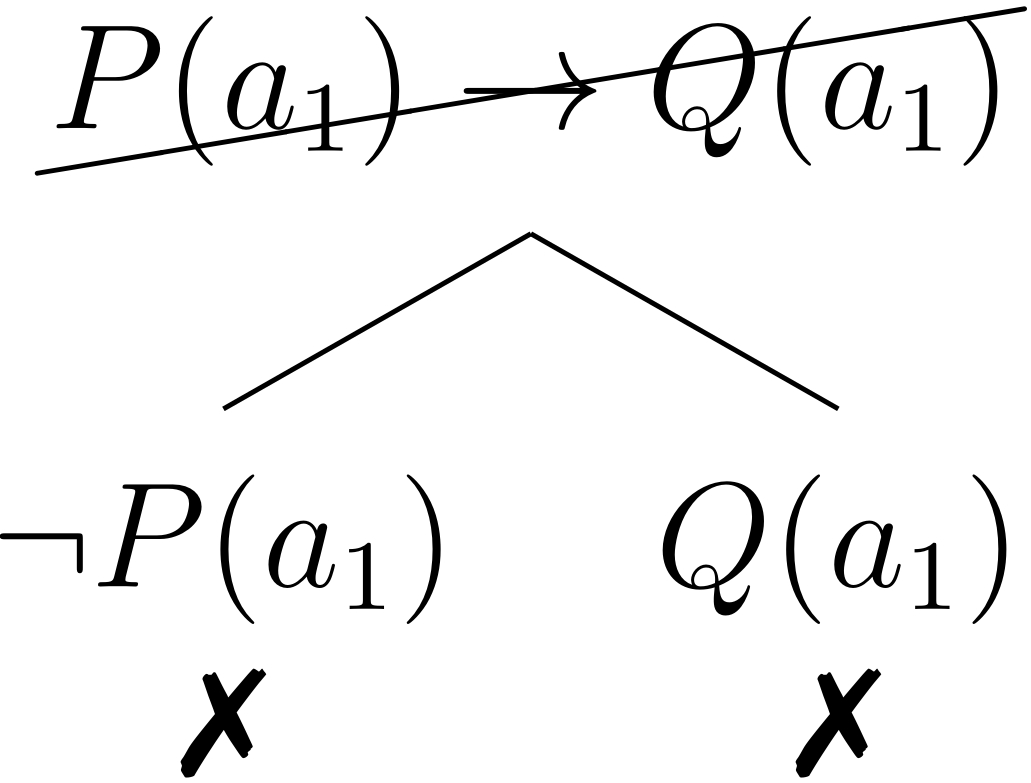
Este ejemplo nos muestra que las fórmulas cuantificadas existencialmente deben ser instanciadas con una constante que represente el elemento del universo que debe existir. Una vez que se introduce una constante o un término cerrado, las fórmulas cuantificadas universalmente se pueden instanciar con dicho elemento.

No use la misma constante dos veces para instanciar fórmulas existenciales

Enseguida se mostrará un intento de construir un tableaux para la negación de la fórmula $\psi =\forall x(P(x)\vee Q(x))\to (\forall xP(x)\vee \forall xQ(x))$, la cual es satisfacible pero no válida. Así que $\neg \psi$ es satisfacible, aunque su tableaux está cerrado. ¿Qué estuvo mal?

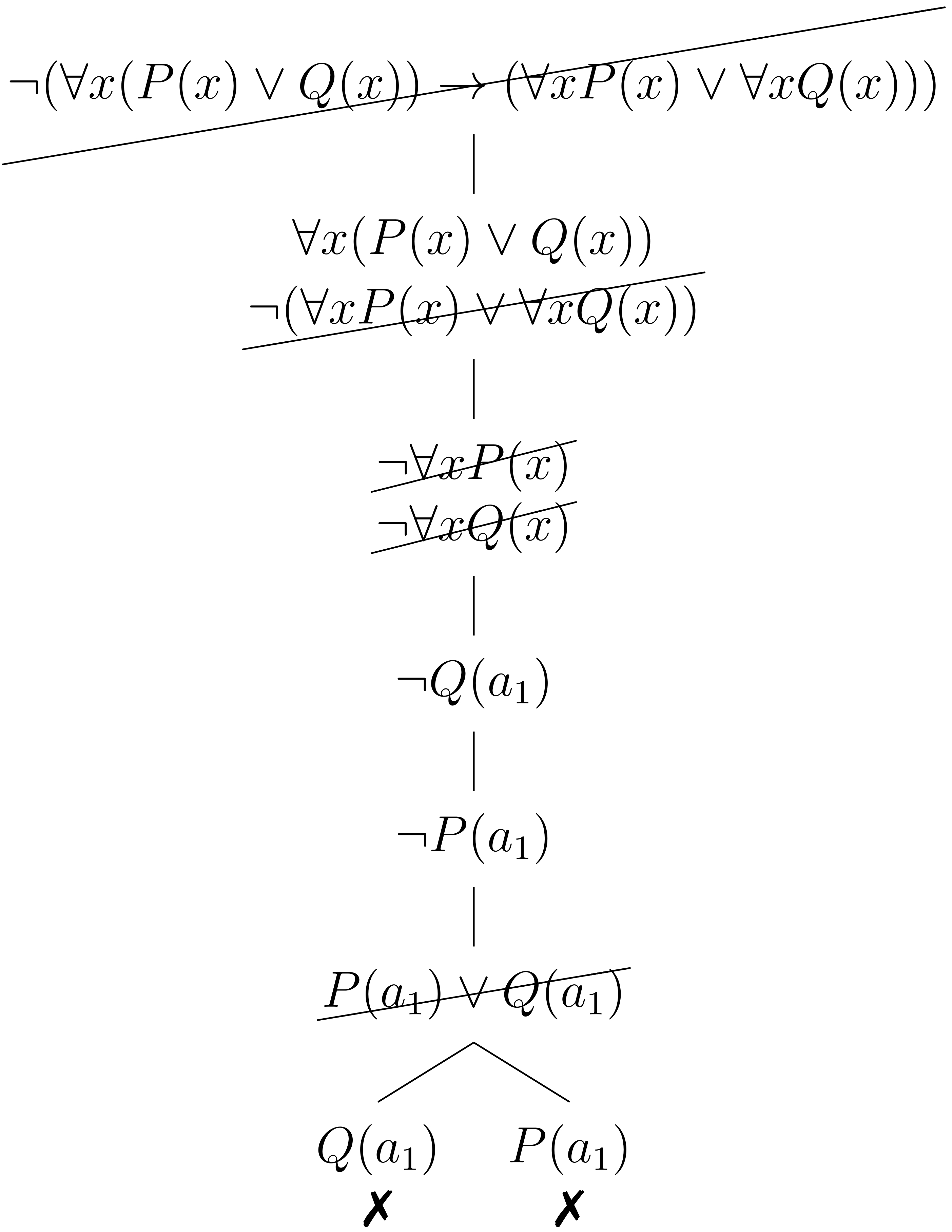
Al instanciar $\neg \forall xP(x)$ no debimos usar la constante $a_1$ ya que fue escogida para instanciar $\neg \forall xQ(x)$. Elegir la misma constante significa que el mismo elemento del universo satisface a ambas fórmulas, lo cual no necesariamente tiene que ser así. De hecho, $\psi$ es verdadera en los modelos que toman como dominio a un solo elemento, pero puede ser insatisfacible para universos con más elementos.

Una nueva constante debe seleccionarse para cada instancia de una fórmula existencial:

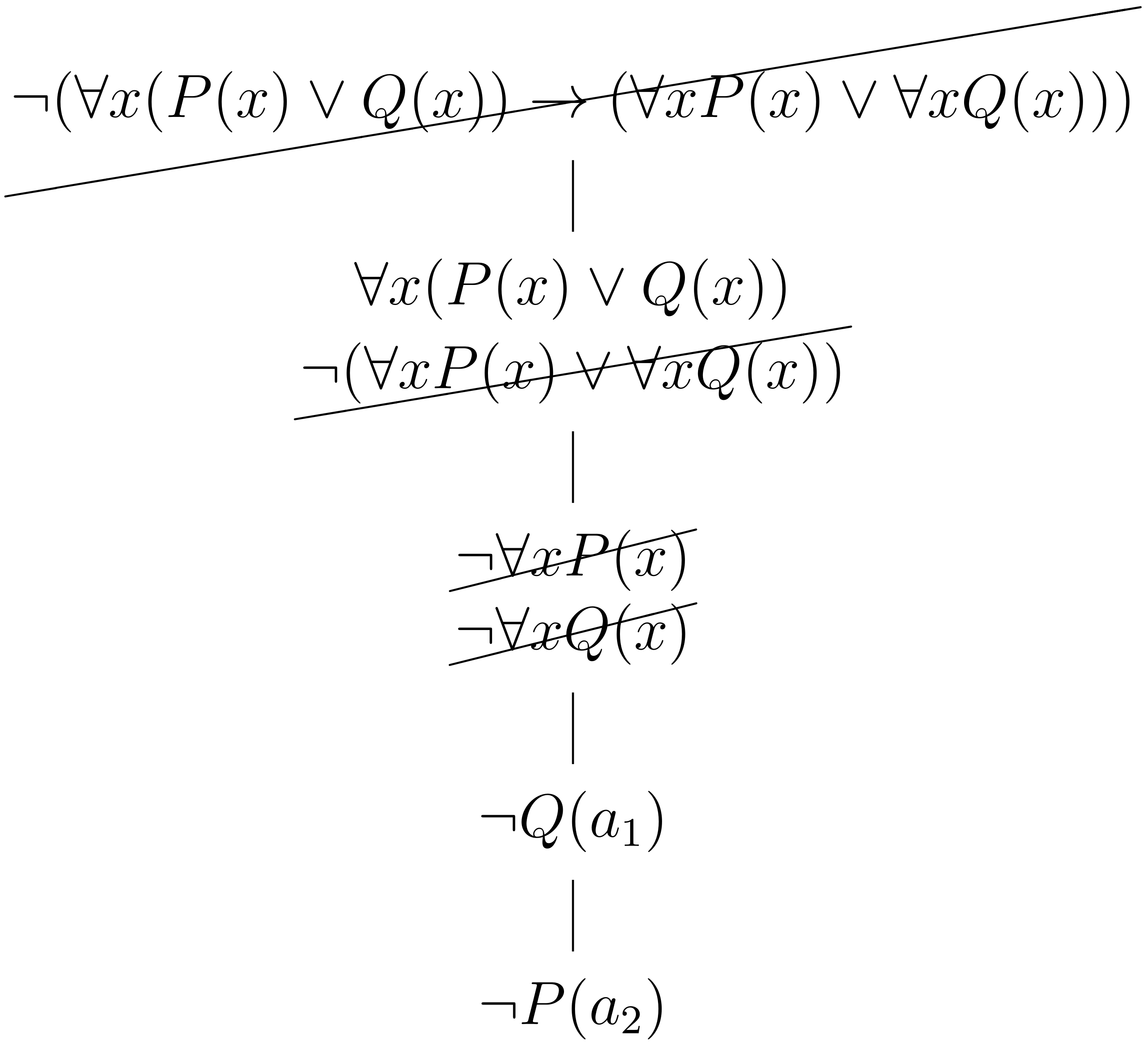
No elimine las fórmulas universales

Siguiendo con el tableaux del ejemplo previo, la fórmula universal $\forall x(P(x)\vee Q(x))$ se tiene que instanciar con $a_1$, y también con $a_2$ ya que debe ser cierta para todos los elementos del universo. De manera que las fórmulas universales nunca son eliminadas del tableaux, permanecen activas todo el tiempo para aplicarse a las nuevas constantes que son introducidas:

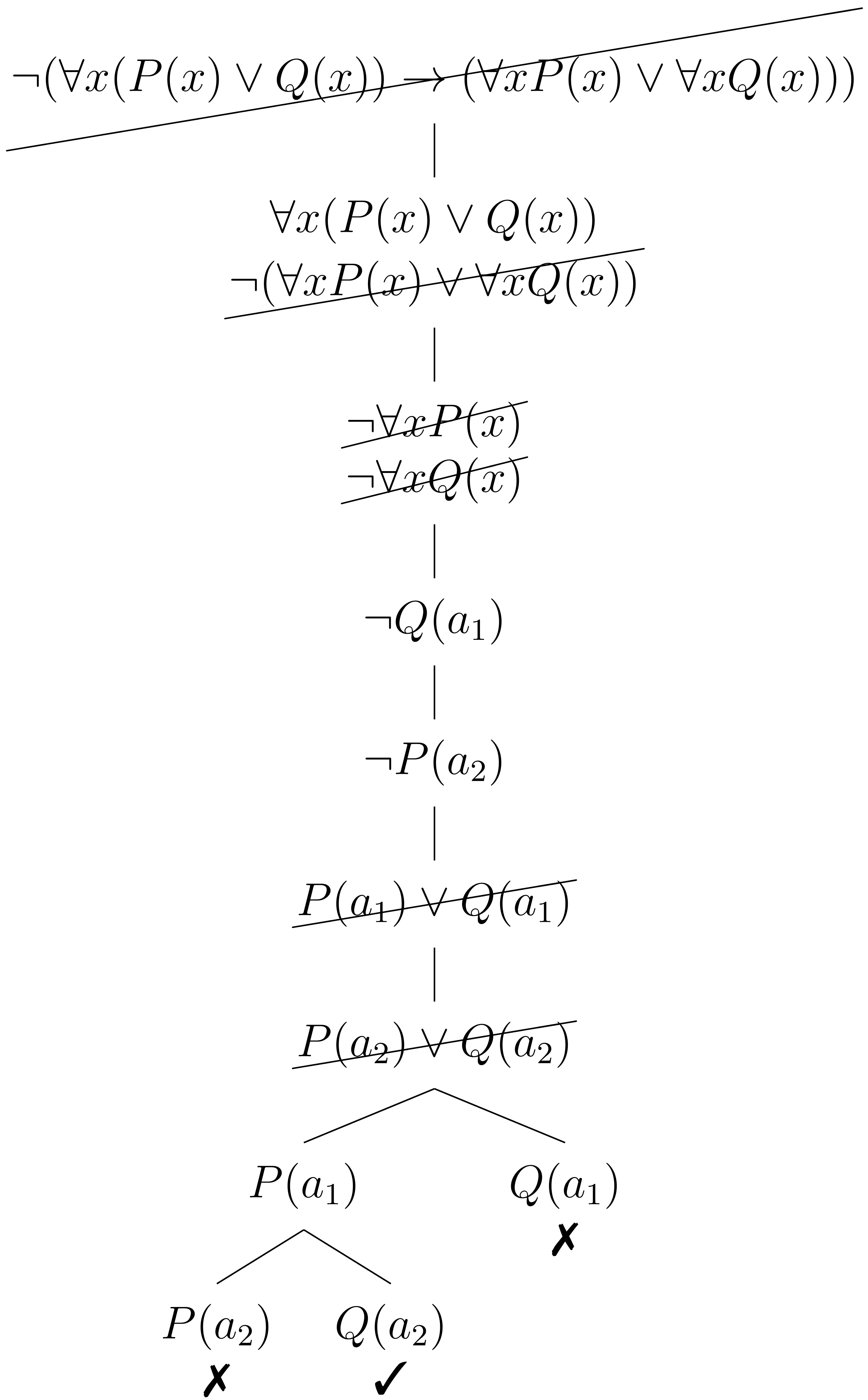
El tableaux quedó abierto. Es posible definir un modelo para $\neg \psi$ tomando un universo con únicamente dos elementos, digamos $A^{ℳ}=\{\mathrm{1,2}\}$, además $a_1^{ℳ}=1$, $a_2^{ℳ}=2$, $P^{ℳ}=\{1\}$ y $Q^{ℳ}=\{2\}$. Un modelo infinito ${ℳ}^{\prime }$ para la misma fórmula considera $A^{{ℳ}^{\prime }}=\mathbb{N}$, $P^{{ℳ}^{\prime }}=\text{“ser par”}$ y $Q^{{ℳ}^{\prime }}=\text{“ser impar”}$. Así ${ℳ}^{\prime }\vDash \neg \psi$, por lo que $\psi$ no es válida.

Una rama puede no terminar

En la nota pasada vimos que la lógica de predicados es indecidible, es decir, no existe algoritmo que determine si una fórmula $\phi$ es válida. Esto implica que, dado un conjunto de fórmulas $\mathrm{\Gamma }$ y una fórmula $\psi$, no existe algoritmo para saber si $\mathrm{\Gamma }\vDash \psi$ o no, puesto que conocer si $\mathrm{\Gamma }\vDash \psi$ es equivalente a determinar si $\mathrm{\Gamma }\to \psi$ es una fórmula válida.

El método de tableaux semánticos no es un procedimiento de decisión para determinar si se satisfacen las fórmulas de la lógica de predicados, ya que no hay manera de conocer si una rama que no se cierra define un modelo infinito o se cerrará en algún momento. Esto se ejemplifica al construir un tableaux semántico para averiguar si la fórmula $\phi =\forall x\exists yP(x,y)$ se satisface. Aparentemente, no se aplican reglas, ya que la fórmula está cuantificada universalmente y solo la instanciamos con términos cerrados que aparecen antes en las fórmulas que etiquetan un nodo.

Sin embargo, recordemos que un modelo define un universo no vacío; por lo tanto, podemos elegir arbitrariamente la constante $a_1$ para representar ese elemento. La construcción del tableaux comienza instanciando $\phi$ y luego instanciando la fórmula existencial con una nueva constante $a_2$.

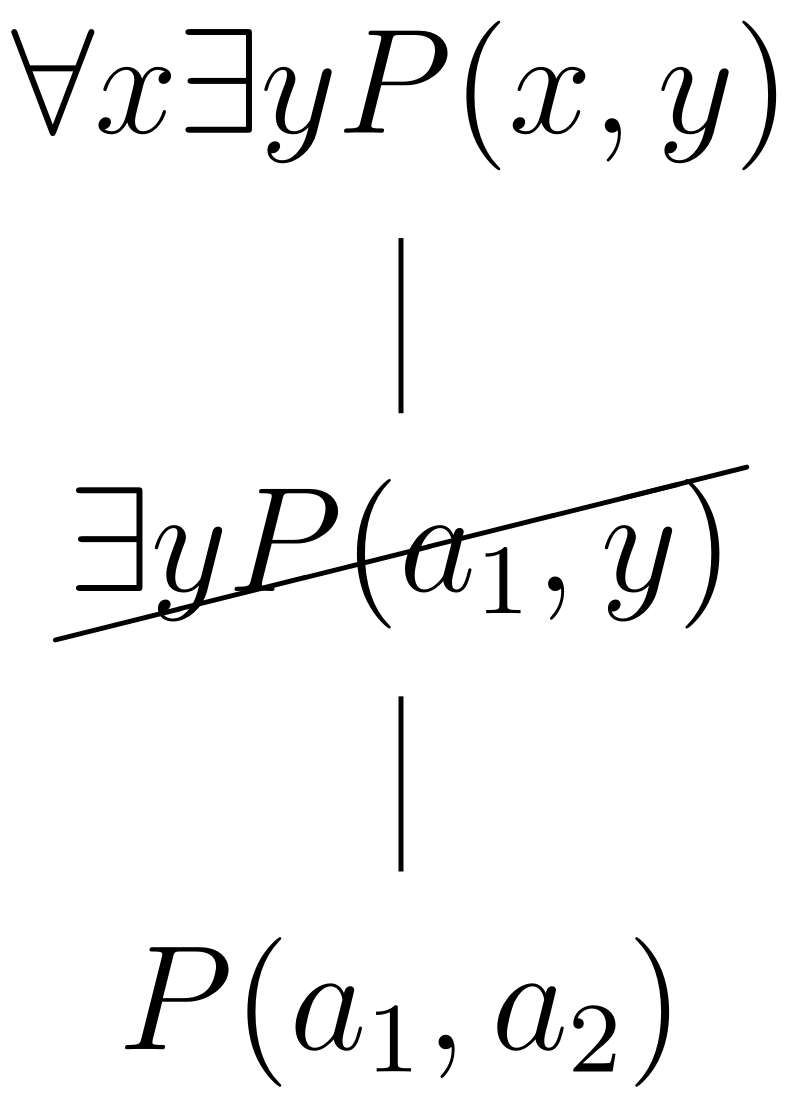
la constante $a_2$ se usa ahora para instanciar de nueva cuenta la fórmula universal $\phi$; esto resulta en una fórmula existencial que es instanciada con una nueva constante $a_3$:

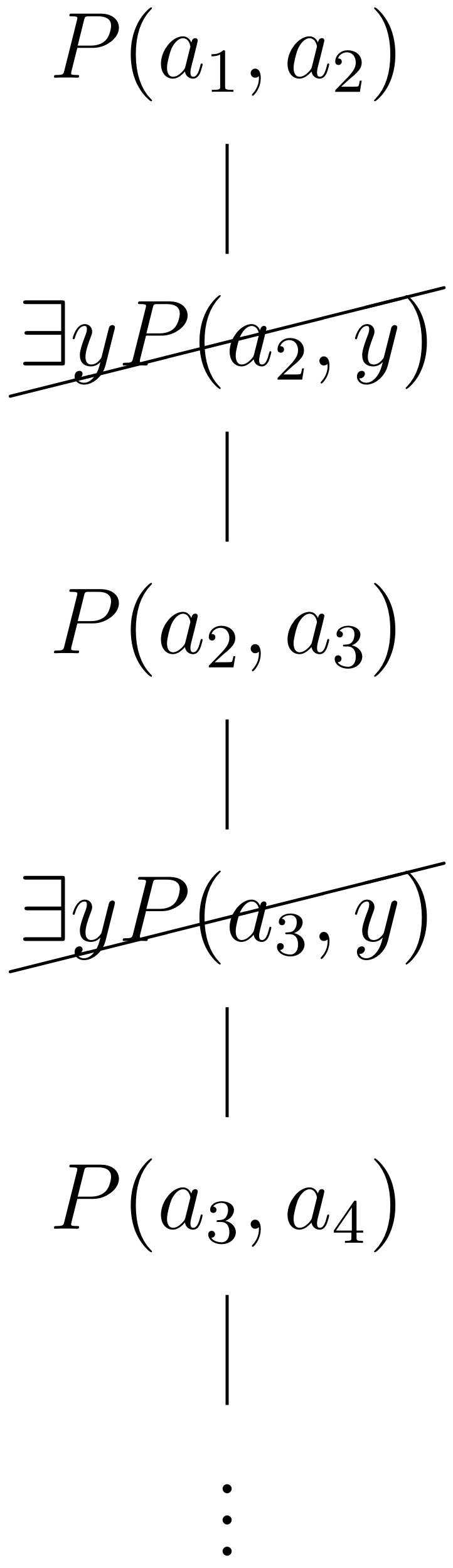
La construcción del tableaux semántico no terminará, dada la rama infinita que se generó. Para $\phi$ se pueden encontrar modelos con universos infinitos; por ejemplo, tome $ℳ$ donde $A\stackrel{def}{=}\mathbb{N}$, y . De igual modo, a $\phi$ la satisfacen modelos finitos, incluso en donde el universo consiste de un solo elemento.

La construcción del tableaux debe ser sistemática

El tableaux que aparece abajo corresponde a la conjunción de $\forall x\exists yP(x,y)$, que ya sabemos que es satisfacible, y de $\forall x(Q(x)\wedge \neg Q(x))$, que no se satisface. Sin embargo, la rama puede continuar indefinidamente, porque estamos eligiendo aplicar reglas sólo a las subfórmulas de $\forall x\exists yP(x,y)$, como hicimos en el ejemplo anterior. Esta rama nunca se cerrará aunque la fórmula sea insatisfacible. Se necesita una construcción sistemática para asegurarse de que las reglas se apliquen a todas las fórmulas que etiquetan un nodo.

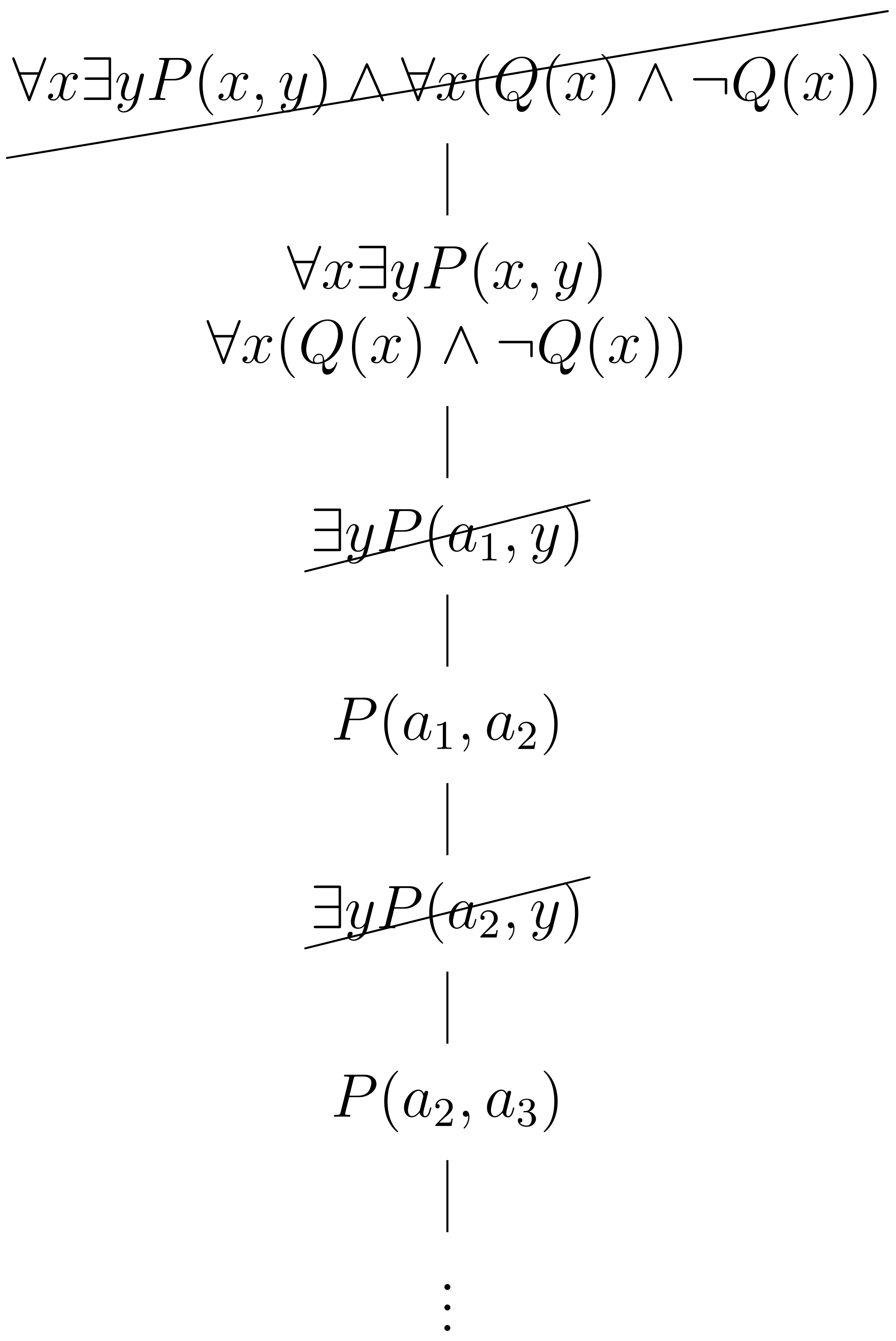
1.2 El algoritmo para construir tableaux semánticos

Definición 1.2.

Una literal cerrada es una fórmula atómica cerrada $P(a_1,\mathrm{\dots },a_n)$, una fórmula atómica cuyos argumentos son términos cerrados, o la negación de una fórmula atómica cerrada $\neg P(a_1,\mathrm{\dots },a_n)$. Si $\mathrm{\ell }$ es $P(a_1,\mathrm{\dots },a_n)$, entonces ${\mathrm{\ell }}^c=\neg P(a_1,\mathrm{\dots },a_n)$, mientras que si $\mathrm{\ell }$ es $\neg P(a_1,\mathrm{\dots },a_n)$, entonces ${\mathrm{\ell }}^c=P(a_1,\mathrm{\dots },a_n)$. Decimos que $\mathrm{\ell }$ y ${\mathrm{\ell }}^c$ son un par de literales cerradas complementarias.

1.3 Clasificación de las fórmulas $\gamma$ y $\delta$

A la clasificación de las fórmulas en $\alpha$ y $\beta$ expuesta en la Nota 04, añadimos las siguientes clasificaciones, donde $c$ es una constante.

1.4 Construcción de tableaux semánticos

Definición 1.3.

Sea $\mathrm{\Gamma }=\{{\phi }_1,\mathrm{\dots },{\phi }_n\}$ un conjunto de fórmulas de la lógica de predicados. Un tableaux para $\mathrm{\Gamma }$, denotado $𝒯(\mathrm{\Gamma })$, es una extensión obtenida recursivamente como sigue:

1. El árbol formado por la rama cuyos nodos son ${\phi }_1,\mathrm{\dots },{\phi }_n$ es una tableaux para $\mathrm{\Gamma }$.

2. Si ${𝒯}^{\prime }$ es un tableaux para $\mathrm{\Gamma }$, la extensión que se obtiene después de aplicarle alguna de las reglas $\alpha$, $\beta$, $\delta$ o $\gamma$ es un tableaux para $\mathrm{\Gamma }$.

3. Es todo.

Definición 1.4.

Una rama de un tableaux está cerrada si en ella figura un par de literales cerradas complementarias. De otro modo, la rama está abierta. Un tableaux está cerrado, si todas sus ramas están cerradas. Si hay una rama abierta, consideramos al tableaux como abierto.

Notemos que una fórmula $\phi$ es válida si y solo si no hay modelo ni ambiente que satisfagan a $\neg \phi$, de manera que el método de tableaux semánticos en la lógica de predicados se usa para demostrar la validez de una fórmula $\phi$ al exhibir un tableaux para $\neg \phi$ que se cierra.

Es importante que al aplicar la construcción descrita en la Definición 1.3 se tome en cuenta lo siguiente:

1. Si $\phi$ es una fórmula a la que se le aplicó una extensión $\alpha$, $\beta$ o $\delta$ en todas las ramas no marcadas, entonces $\phi$ se considera inactiva y no puede tomarse nuevamente para una extensión.

2. La regla $\gamma$ puede utilizarse para realizar una extensión cualquier número de veces, utilizando distintos términos cerrados en cada ocasión. La regla $\gamma$ permanece siempre activa.

3. No se debe usar la misma constante dos veces para instanciar fórmulas existenciales.

4. Cualquier extensión de una fórmula $\phi$ debe realizarse sobre todas las ramas no marcadas del tableaux en la que $\phi$ está activa, y únicamente sobre éstas.

5. Se prefiere la aplicación de la regla $\alpha$ sobre la regla $\beta$. Adicionalmente, se busca aplicar la regla $\delta$ antes que la regla $\gamma$.

6. El uso de la regla $\gamma$ se debe posponer hasta que sea estrictamente necesario.

7. La regla $\gamma$ debe utilizar en su extensión términos cerrados ya presentes, a menos de que no existan.

1.5 El método de tableaux semánticos es correcto y completo

El método de tableaux es correcto como lo anuncia el siguiente teorema.

Teorema 1.5.

Si hay un tableaux cerrado para $\mathrm{\Gamma }$, entonces $\mathrm{\Gamma }$ no tiene un modelo.

Este método también es completo con respecto a la refutación.

Teorema 1.6.

Si $\mathrm{\Gamma }$ no tiene un modelo, entonces existe un tableaux $𝒯(\mathrm{\Gamma })$ cerrado.

De lo anterior se desprende el siguiente corolario con el que relacionamos a los tableaux semánticos con la consecuencia lógica.

Corolario 1.7.

$\mathrm{\Gamma }\vDash \phi$ syss podemos obtener un tableaux $𝒯(\mathrm{\Gamma }\cup \{\neg \phi \})$ que sea cerrado.

1.6 Ejemplo

Determine si el argumento lógico correcto $\{\forall x\forall y\left(P(x)\to (Q(x)\wedge R(y))\right),P(c)\}\vDash \neg \left(\forall z\neg Q(z)\right)$ es correcto.

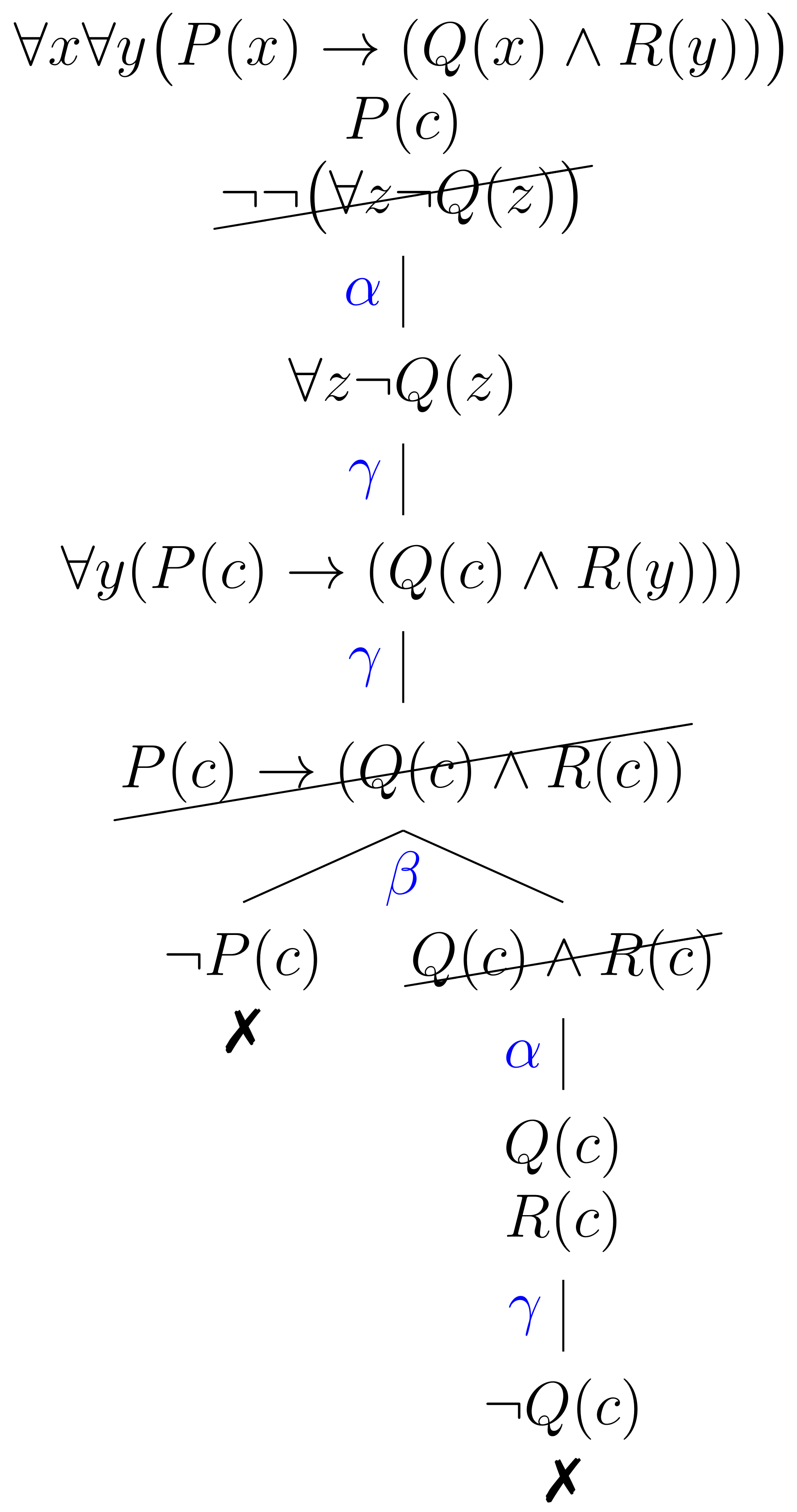
Como el tableaux se cerró, el principio de refutación indica que el argumento lógico es correcto.

2 Ejercicios

1. Determine si las siguientes fórmulas son válidas a través de un tableaux semántico.

   • $\forall x\left(P(x)\vee Q(x)\right)\to \forall xP(x)\vee \forall xQ(x)$,

   • $\forall x\left(P(x)\to Q(x)\right)\to \left(\exists xP(x)\to \exists xQ(x)\right)$.

2. Determine si los siguientes conjuntos de fórmulas son satisfacibles a través de un tableaux semántico.

   • $\{\forall x\neg P(x),\exists x\left(P(x)\vee \neg P(f(x))\right)\}$,

   • $\{P(a),\forall x\left(P(x)\wedge \neg P(f(x))\right)\}$,

   • $\{\forall x\neg P(x,a),P(a,b),\forall x\forall y\left(\neg P(x,y)\vee P(y,x)\right)\}$.

3. Decida mediante un tableaux semántico si los siguientes argumentos son correctos.

   • $\{\forall x\left(P(x)\to Q(x)\vee R(x)\right),\neg \exists x\left(P(x)\wedge R(x)\right)\}\vDash \forall x\left(P(x)\to Q(x)\right)$,

   • $\{\forall x\left(P(x)\vee Q(x)\right),\exists x\neg Q(x),\forall x\left(R(x)\to \neg P(x)\right)\}\vDash \exists x\neg R(x)$,

   • $\{\forall x\forall y\forall z\left(P(x,y)\wedge P(y,z)\to P(x,z)\right),\forall x\forall y\left(P(x,y)\to P(y,x)\right)\}\vDash \forall x\forall y\forall z\left(P(x,y)\wedge P(z,y)\to P(x,z)\right)$,

   • $\{\forall xA(a,x,x),\forall x\forall y\forall z\left(A(x,y,z)\to A(x,s(y),s(z))\right),\forall x\forall y\forall z\left(A(x,y,z)\to A(y,x,z)\right)\}$$\vDash \exists xA(s(s(a)),s(a),x)$.