Detection of tube-like structures using multiscale analysis has been carried out by other researchers [16,17,18]. The main purpose of these works is to develop a line-enhancement filter based on the eigenvalue analysis of the Hessian matrix. These filters were applied to 2-D and 3-D medical images such as digital subtraction angiography or magnetic resonance angiography of blood vessels and computer tomography of airways. We use similar information in combination with gradient information to segment blood vessels rather than to enhance them.
Gradient magnitude. The magnitude of the gradient
![]() ,
represents the slope of the image intensity for a particular value of
the parameter s.
Figure 3 shows the gradient magnitude at different scales
for the subimages shown in Figure 2.
,
represents the slope of the image intensity for a particular value of
the parameter s.
Figure 3 shows the gradient magnitude at different scales
for the subimages shown in Figure 2.
Principal curvature. The second directional derivatives
describe the variation in the gradient of intensity in the
neighbourhood of a point.
Since vessels appear as ridge-like structures in the images, we
look for pixels where the
intensity image has a local maximum in the direction for which the
gradient of the image undergoes the largest change (largest
concavity) [19].
The second derivative information is
derived from the Hessian of the intensity image ![]() :
:
 |
In order to analyse both red-free and fluorescein images with the same algorithm,
we define
![]() and
and
![]() .
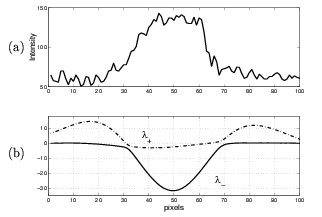
The maximum eigenvalue,
.
The maximum eigenvalue, ![]() , corresponds to
the maximum principal curvature of the Hessian tensor, which we will
refer to as maximum principal curvature.
Thus, a pixel belonging to a vessel region will be
weighted as a vessel pixel if
, corresponds to
the maximum principal curvature of the Hessian tensor, which we will
refer to as maximum principal curvature.
Thus, a pixel belonging to a vessel region will be
weighted as a vessel pixel if
![]() ,
for both red-free and fluorescein images.
Figure 5 shows the maximum principal curvature
,
for both red-free and fluorescein images.
Figure 5 shows the maximum principal curvature
![]() at different scales for the subimages shown in
Figure 2.
at different scales for the subimages shown in
Figure 2.